- 利用导数求参数的取值范围
- 共134题
点(x,y)满足
正确答案
解析
实数x,y满足不等式组 
由图可知,当x=a,y=1﹣a时,
目标函数z=x﹣2y取得最大值,
即1=a﹣2×(1﹣a),解得:a=1
故选A。
知识点
过点

正确答案
解析
圆的标准方程是:(x+1)2+(y-2)2=132,圆心(-1,2),半径r=13过点
A(11,2)的最短的弦长为10,最长的弦长为26,(分别只有一条)还有长度为11,12,…,25的各2条,所以共有弦长为整数的2+2×15=32条,故选C
知识点
20.已知函数f(x)=
(1)当a=1时,求f(x)的最小值;
(2)若f(x)在(0,e]上的最小值为2,求实数a的值;
(3)当a=﹣1时,试判断函数g(x)=f(x)+
正确答案
(1)1
(2)a=e
(3)见解析。
解析
(1)当a=1时,
当x∈(0,1)时,f′(x)<0,f(x)单调递减,
当x∈(1,+∞)时,f′(x)>0,f(x)单调递增,
所以,当x=1时,f(x)有最小值:f(x)min=f(1)=1.
(2)因为
①当a≤0时,f′(x)>0,f(x)在(0,e]上为增函数,此时f(x)在(0,e]上无最小值.
②当a∈(0,e]时,若x∈(0,a),则f′(x)<0,f(x)单调递减,
若x∈(a,e],则f′(x)>0,f(x)单调递增,
所以f(x)min=f(a)=1+lna=2,∴a=e,符合题意;
③当a>e时,x∈(0,e],
∴f′(x)<0,f(x)单调递减,
所以
∴a=e,不符合题意;
综上所述,a=e时符合题意.
(3)证明:当a=﹣1时,函数

令φ(x)=2+x﹣lnx,(x>0),则
所以x∈(0,1)时,φ′(x)<0,φ(x)单调递减,
当x∈(1,+∞)时,φ′(x)>0,φ(x)单调递增,
所以,φ(x)min=φ(1)=3>0,在定义域内g′(x)>0,g(x)在(0,+∞)单调递增,
又g(1)=﹣1<0,而
因此,函数g(x)在(1,e)上必有零点,又g(x)在(0,+∞)单调递增,
所以函数
知识点
17.已知函数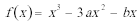
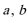
(1)若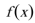
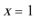
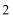
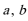
(2)若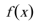
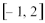
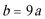
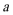
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数

(1)求
(2)不等式




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析



