- 利用导数求参数的取值范围
- 共134题
1
题型:简答题
|
20.设

(1)若

(2)若函数



(3)若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
导数的几何意义利用导数研究函数的单调性利用导数求函数的极值利用导数求参数的取值范围
1
题型:简答题
|
22.设函数
(1)当
(2)若函数
(3)若对于任意的

正确答案
解:(1)
当
令
当

所以
在区间
(2)

则方程

这时,
因此满足条件的
(3)由(2)知,当
当
因此函数
又
于是
因此满足条件的
解析
解析已在路上飞奔,马上就到!
知识点
利用导数研究函数的单调性利用导数求函数的极值利用导数求函数的最值利用导数求参数的取值范围
1
题型:简答题
|
21.已知函数


(Ⅰ)讨论
(Ⅱ)若

(Ⅲ)设函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
利用导数研究函数的单调性利用导数求函数的最值利用导数求参数的取值范围
1
题型:简答题
|
20. 设函数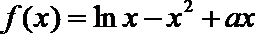
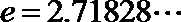
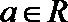
(Ⅰ)当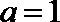
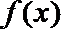
(Ⅱ)若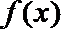
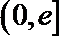
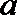
(Ⅲ)设函数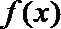
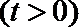
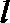
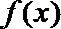
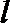
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
导数的几何意义利用导数研究函数的单调性利用导数求函数的极值利用导数证明不等式利用导数求参数的取值范围
1
题型:简答题
|
19.定义在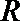
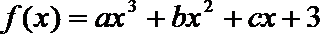
① 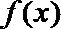
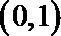
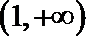
② 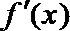
③ 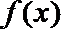
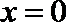
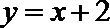
(1)求函数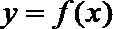
(2)设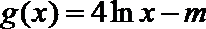
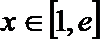
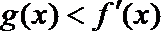
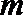
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
导数的几何意义导数的运算利用导数研究函数的单调性利用导数求参数的取值范围
下一知识点 : 生活中的优化问题举例
扫码查看完整答案与解析