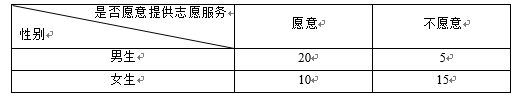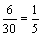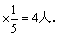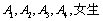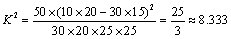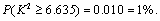- 生活中的几何概型问题
- 共10题
24.在谈到某些图书的价格时,有人认为:“每一份的品质都是由每一份的成本堆积起来的,没有真正物美价廉的东西。”这一观点蕴含的经济道理是( )
正确答案
解析
解析已在路上飞奔,马上就到!
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
某村庄拟修建一个屋盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为






(1)将


(2)讨论函数


正确答案
见解析
解析
(1)因为蓄水池侧面的总成本为100·2πrh=200πrh元,底面的总成本为160πr2元,所以蓄水池的总成本为(200πrh+160πr2)元。
又据题意200πrh+160πr2=12 000π,
所以h=
从而V(r)=πr2h=
因r>0,又由h>0可得
故函数V(r)的定义域为(0,
(2)因V(r)=
故V′(r)=
令V′(r)=0,解得r1=5,r2=-5(因r2=-5不在定义域内,舍去)。
当r∈(0,5)时,V′(r)>0,故V(r)在(0,5)上为增函数;
当r∈(5,

由此可知,V(r)在r=5处取得最大值,此时h=8.
即当r=5,h=8时,该蓄水池的体积最大。
知识点

正确答案
解析
略
知识点
2014年山东省第二十三届运动会将在济宁召开,为调查我市某校高中生是否愿意提供志愿者服务,用简单随机抽样方法从该校调查了50人,结果如下:
(1)用分层抽样的方法在愿意提供志愿者服务的学生中抽取6人,其中男生抽取多少人?
(2)在(I)中抽取的6人中任选2人,求恰有一名女生的概率;
(3)你能否有99%的把握认为该校高中生是否愿意提供志愿者服务与性别有关?
下面的临界值表供参考:
独立性检验统计量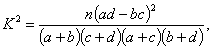
正确答案
见解析。
解析
(1)在愿意提供志愿者服务的学生中抽取6人,则抽取比例为
所以男生应该抽取20
(2)在(1)中抽取的6名学生中,女生有2人,男生有4人,男生4人记为
2人记为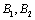
……共15种情况。
(3)因为
且
所以能用99%的把握认为是否愿意提供志愿者服务是与性别有关系的。
知识点
高三年级进行模拟考试,某班参加考试的40名同学的成绩统计如下:
规定分数在90分及以上为及格,120分及以上为优秀,成绩高于85分低于90分的同学为希望生.已知该班希望生有2名.
(1)从该班所有学生中任选一名,求其成绩及格的概率;
(2)当a =11时,从该班所有学生中任选一名,求其成绩优秀的概率;
(3)从分数在(70,90)的5名学生中,任选2名同学参加辅导,求其中恰有1名希望生的概率.[来源:学,科,网]
正确答案
(1)
(2)
(3)
解析
(1)设“从该班所有学生中任选一名,其成绩及格”为事件A,则

(2)设“从该班所有学生中任选一名,其成绩优秀”为事件B,则当


(3)设“从分数在
记这5名学生分别为a,b,c,d,e,其中希望生为a,b.
从中任选2名,所有可能的情况为:ab, ac, ad, ae,bc,bd,be,cd,ce,de,共10种. ………9分
其中恰有1名希望生的情况有ac, ad, ae,bc,bd,be,共6种.………11分
所以
知识点
设双曲线


正确答案
解析
由双曲线方程可知渐近线方程为

知识点
某校共有学生2000名,各年级男、女学生人数如右表所示,已知在全校学生中随机抽取1名,抽到高二级女生的概率是0.19,现用分层抽样的方法(按年级分层)在全校学生中抽取64人,则应在高三级中抽取的学生人数为 。
正确答案
16
解析
略
知识点
定义:如果函数y=f(x)在定义域内给定区间








正确答案
解析
略
知识点
扫码查看完整答案与解析