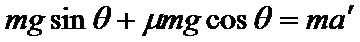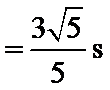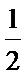- 机械能
- 共1183题
7.两个圆管道的半径均为R,通过直管道将它们无缝连接在一起.让一直径略小于管径的小球从入口A处无初速度放入,B、C、D是轨道上的三点,E为出口,其高度略低于入口A.已知BC连线经过右侧圆管道的圆心,D点与圆管道的圆心等高,以下判断正确的有( )
(在每小题给出的四个选项中,至少有一个选项是正确,全部选对的得6分,选对但不全的得3分,不选或有选错的得0分。)
正确答案
解析
解:A、由于小球在D点做圆周运动,所以知管道左侧受到小球的压力, 故A错误;
B、若光滑,则A到E过程中机械能守恒,所以小球能从E点射出.故B正确;
C、若不光滑,小球到达C点的速度不确定,管道对小球的作用力可能为0,故C正确。
D、只要A、E间高度差足够大,足以克服摩擦力做功就有可能从E点射出,故选项D错误;
故选:BC
考查方向
解题思路
A. 让小球在竖直放置的空心粗糙塑料管中运动,利用牛顿第二定律与圆周运动的向心力公式,可求出某点的受力情况.
B. 同时运用动能定理,可找出某两点的速度与这两点的高度关系.
C. 小球从高于E点的A点静止释放,若光滑时则由机械能守恒定律,可得出小球是否能从E点射出.
D. 当小球到达最高点C时,由速度结合牛顿第二定律可得出小球的受力情况.
易错点
在管中的列动能定理不会求重力做功对应的高度差,以及圆管中水平和竖直的四个点的临界速度
知识点
如图所示,光滑水平面上依次放置两个质量均为m的小物块A和C以及光滑曲面劈B,B的质量为M=3m,劈B的曲面下端与水平面相切,且劈B足够高。现让小物块C以水平速度v0向右运动,与A发生弹性碰撞,碰撞后小物块A又滑上劈B。求物块A在B上能够达到的最大高度。
正确答案
解析
小物块C与A发生弹性碰撞,由动量守恒和机械能守恒得:


联立①②式解得:

设小物块A在劈B上达到的最大高度为h,此时小物块A和B的共同速度大小为v,对小物块A与B组成的系统,由机械能守恒和水平方向动量守恒得:


联立③④⑤式

考查方向
本题考查了应用动量守恒定律与机械能守恒定律的应用。
解题思路
A、C系统碰撞过程动量守恒,机械能守恒,应用动量守恒定律与机械能守恒定律求出A的速度; A、B系统在水平方向动量守恒,由动量守恒定律与机械能守恒定律可以解题。
易错点
A与B相互时,系统水平方向不受外力,水平方向动量守恒,注意动量守恒定律的应用条件。
知识点
20.如图,由同种材料制成的三个斜面a、b、c,底边长分别为L、L、2L,高度分别为2h、h、h。现将一可视为质点的物块分别从三个斜面的顶端由静止释放,在物块沿斜面下滑到底端的过程中,下述可能正确的是
正确答案
解析
A、设任一斜面的倾角为α,斜面的长度为S.根据牛顿第二定律得:mgsinα﹣μmgcosα=ma,得 a=gsinα﹣μgcosα,则可能有aa>ab>ac.故A正确.
B、由S=

C、对物体在任一斜面上滑动的过程,由动能定理得:
mgSsinα﹣μmgcosα•S=Ek,式中Ssinα等于斜面的高度,Scosα等于斜面底边的长度.
则 Eka=mg•2h﹣μmgL=2mgh﹣μmgL,Ekb=mgh﹣μmgL,Ekc=mgh﹣μmg•2L=mgh﹣2μmgL,由数学知识可知,不可能有:Eka=2Ekb=4Ekc.故C错误.
D、根据功能关系知,物块损失的机械能等于克服摩擦力做功,则有△ E=μmgcosα•S,Scosα等于斜面底边的长度.因此有△ Ec=2μmgL,△ Eb=μmgL,△ Ea=μmgL,所以△ Ec=2△ Eb=2△ Ea.故D正确.
考查方向
解题思路
物块的加速度可根据牛顿第二定律列式分析.运动时间由位移时间公式列式.可根据动能定理分析物体到达底端时动能关系.比较克服摩擦力做功的大小,由功能关系分析损失的机械能关系.
易错点
本题求克服摩擦力做功可推得一个重要的结论:物体从斜面下滑到底端的过程中,克服摩擦力做的功与沿水平面滑动与斜面底端相同距离时克服摩擦力做的功相同
知识点
23.图中虚线所示为静电场中的等势面1、2、3、4,相邻的等势面之间的电势差相等,其中等势面3的电势为零。一带正电的点电荷在静电力的作用下运动,经过
正确答案
10 16
解析
经过a、b点时的动能分别为24eV和3eV;
图中虚线所示为静电场中的等势面1、2、3、4,相邻的等势面之间的电势差相等,
故电荷经过相邻两个等势面时的动能减小量为△Ek=
只有电场力做功,电势能和动能之和守恒,其电势能变为﹣6eV时,故有:0eV+10eV=﹣6eV+Ek;
解得:Ek=16eV.
考查方向
解题思路
只有电场力做功,电势能和动能之和守恒,根据题意曲线3处的电势为零,列式求解点电荷的电势能与动能的和,然后结合功能关系即可求出动能.
易错点
在只有电场力做功的条件下动能和电势能的总和保持不变;相邻等势面之间的电势差相同
知识点
如图,倾角θ=30°的光滑斜面底端固定一块垂直于斜面的挡板。将长木板A静置于斜面上,A上放置一小物块B,初始时A下端与挡板相距L=4m,现同时无初速释放A和B。已知在A停止运动之前B始终没有脱离A且不会与挡板碰撞,A和B的质量均为m=1kg,它们之间的动摩擦因数μ=
26.A第一次与挡板碰前瞬间的速度大小v;
27.A第一次与挡板碰撞到第二次与挡板碰撞的时间△t;
28.B相对于A滑动的可能最短时间t。
正确答案
解析
解:B和A一起沿斜面向下运动,由机械能守恒定律有
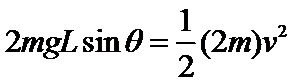
由①式得 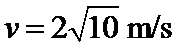
考查方向
解题思路
1、分析A与B之间的最大静摩擦力的大小,分析A、B是否会相对滑动。2、利用受力分析和功能关系求出A第一次与挡板碰前瞬间的速度大小。3、由对A再次受力分析,利用运动学公式和功能关系求得间隔时间。4、根据对B在单独分析得到相对滑动的最短时间。
易错点
对两物体发生相对滑动的条件不清楚。
正确答案
解析
解: 第一次碰后,对B有
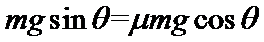
对A有

得A的加速度 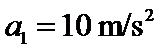
设A第1次反弹的速度大小为v1,由动能定理有
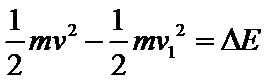

由⑥⑦式得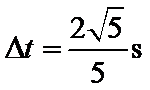
考查方向
解题思路
1、分析A与B之间的最大静摩擦力的大小,分析A、B是否会相对滑动。2、利用受力分析和功能关系求出A第一次与挡板碰前瞬间的速度大小。3、由对A再次受力分析,利用运动学公式和功能关系求得间隔时间。4、根据对B在单独分析得到相对滑动的最短时间。
易错点
对两物体发生相对滑动的条件不清楚。
正确答案
解析
解: 设A第2次反弹的速度大小为v2,由动能定理有
得
即A与挡板第2次碰后停在底端,B继续匀速下滑,与挡板碰后B反弹的速度为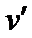
加速度大小为a′,
由动能定理有
B沿A向上做匀减速运动的时间
当B速度为0时,因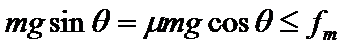
当A停止运动时,B恰好匀速滑至挡板处,B相对A运动的时间t最短,故
考查方向
解题思路
1、分析A与B之间的最大静摩擦力的大小,分析A、B是否会相对滑动。2、利用受力分析和功能关系求出A第一次与挡板碰前瞬间的速度大3、由对A再次受力分析,利用运动学公式和功能关系求得间隔时间4、根据对B在单独分析得到相对滑动的最短时间。
易错点
对两物体发生相对滑动的条件不清楚。
如图所示,在竖直平面xOy内,x轴的下方存在匀强电场

19.求电场强度的大小
20.求小滑块从A点开始运动到原点O的过程中克服摩擦力做的功。
21.求小滑块从管口射出后的最小速度。
正确答案

解析
小滑块在管内匀速运动时,有q=mg+f
又f=μN=μq v0B
解得:

考查方向
解题思路
最大速度是指合力为零,所以对C点受力分析,从而求出电场力,进而求出电场强度。
易错点
最大速度是指加速度为零时的速度。
正确答案
Wf =1×10-6J。
解析
小滑块从A点运动到O点的过程中,根据动能定理,有:
小滑块克服摩擦力做功:
考查方向
解题思路
摩擦力是变力,求摩擦力做功就只能用动能定理解决。
易错点
摩擦力做功是变力做功,所以要用动能定理。
正确答案
vmin=3 m/s
解析
小滑块从管口射出后,在水平方向做初速度为零的匀加速运动,
其加速度大小 
加速度大小等于g=10m/s2
经过任意t时间,小滑块的速度
代入数据整理得:
当t=0.32s时,小滑块速度最小,并且最小速度:vmin=3 m/s。
考查方向
解题思路
在水平电场中,分析运动情况,可知在水平方向上做匀加速运动,在竖直方向上做匀减速运动,用运动的合成和分解,通过数学方法求最小值,即可求出答案。
易错点
最小速度是指合速度最小,运用运动的合成和分解列出数学表达式。
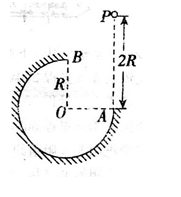
17.如图所示,在竖直平面内有一半径为R的圆弧轨道,半径OA水平、OB竖直,一个质量为m的小球自A的正上方P点由静止开始自由下落,小球恰好能沿轨道到达最高点B。已知AP=2R,重力加速度为g,则小球从P到B的运动过程中
正确答案
解析
:A、重力做功WG=mg(2R-R)=mgR,故A错误;
B、小球沿轨道到达最高点B时恰好对轨道没有压力,则有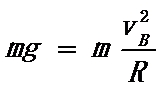
则机械能减少量为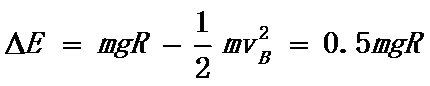
C、根据动能定理得:合外力做功 
D、根据功能原理可知,克服摩擦力做功等于机械能的减少,为0.5mgR,故D错误;
故选:B
考查方向
解题思路
重力做功只跟高度差有关,只有重力或弹簧弹力做功时,机械能守恒,根据动能定理求解合外力做的功及摩擦力做的功。
易错点
理解功是能量转化的量度,克服摩擦力做功等于机械能的减少。
知识点
如图所示,某货场需将质量为m的货物(可视为质点)从高处运送至地面,现利用固定于地面的倾斜轨道传送货物,使货物由轨道顶端无初速滑下,轨道与水平面成θ=37°角。地面上紧靠轨道依次排放两块完全相同木板A、B,长度均为l=2m,厚度不计,质量均为m,木板上表面与轨道末端平滑连接。货物与倾斜轨道间动摩擦因数为μ0=0.125,货物与木板间动摩擦因数为μ1,木板与地面间动摩擦因数μ2=0.2。回答下列问题:(最大静摩擦力与滑动摩擦力大小相等,sin37°=0.6,cos37°=0.8,g=10m/s2)
27.若货物从离地面高h0=1.5m处由静止滑下,求货物到达轨道末端时的速度v0;
28.若货物滑上木板A时,木板不动,而滑上木板B时,木板B开始滑动,求μ1应满足的条件;
29.若μ1=0.5,为使货物恰能到达B的最右端,货物由静止下滑的高度h应为多少?
正确答案
5m/s ;
解析
货物在倾斜轨道上的受力如图,由牛顿第二定律:
mgsinθ- μmgcosθ=ma0 代入数据解得a0=5m/s2
由运动学公式:
考查方向
解题思路
货物下滑时根据牛顿第二定律求出下滑时的加速度,再根据速度位移关系求出到达末端时的速度;
易错点
由于是两块木板,货物运动到不同的地方时木板的受力不一样,所以当货物滑上木板后正确的受力分析是关键。
正确答案
解析
若滑上木板A时,木板不动,由受力分析得
若滑上木板B时,木板B开始滑动,由受力分析得
考查方向
解题思路
根据木板动与不动的条件求解货物与木板间的动摩擦因数所满足的条件;
易错点
由于是两块木板,货物运动到不同的地方时木板的受力不一样,所以当货物滑上木板后正确的受力分析是关键。
正确答案
2.64m;
解析
由(2)知货物滑上A时,木板不动,而滑上木板B时,木板B开始滑动.
货物下滑高度记为h2,到达斜道末端时速度记为v2,
货物滑上A时做匀减速运动,加速度大小a1=gμ1=5m/s2
货物离开A时速度记为v3,
货物滑上B时,自身加速度大小a2=gμ1=5m/s2,
B的加速度大小a3=gμ1-2gμ2=1m/s2
由题意,货物到达B最右端时两者恰好具有共同速度,记为v4
货物做匀减速运动:
B做匀加速运动:
位移关系满足:
代入数据解得:h2=2.64m
考查方向
解题思路
根据28中条件求解μ1=0.5时货物在A、B上运动情况由运动学公式求得货物静止时下滑的高度h
易错点
由于是两块木板,货物运动到不同的地方时木板的受力不一样,所以当货物滑上木板后正确的受力分析是关键。
如图,直角坐标系xOy的y轴竖直向上,在整个空间区域 内存在平行于xOy平面的匀强电场,在y<0的区域内还存在垂直

24.O、P两点间的电势差UOP;
25.匀强电场的场强E的大小和方向。
正确答案
解析
考查方向
解题思路
1、有动能定理求得O、P两点的电势差。2、可求出O、P、Q三点的电势然后找出等势点,由电场场强方向垂直于等势线可得到场强。
易错点
动能定理运用时,正负问题。
正确答案

解析
带电小颗粒从O到Q,由动能定理有

由③式得
如图,由几何关系得:P点到OQ连线的距离d=0.4 m ④
根据匀强电场中场强与电势差关系得

电场方向与OQ连线垂直,沿左上方。
考查方向
解题思路
1、有动能定理求得O、P两点的电势差。2、可求出O、P、Q三点的电势然后找出等势点,由电场场强方向垂直于等势线可得到场强。
易错点
动能定理运用时,正负问题。
13.如图所示,小球从A点以初速度v0沿粗糙斜面向上运动,到达最高点B后返回A,C为AB的中点。则小球从A到C与从C到B的过程中正确的是( )
正确答案
解析
由动能定理得,A到C和C到B的过程中,合外力做功相等,所以动能变化量相等,所以C错;但是动能变化量是速度的平方差,不等于速度差的平方,所以A错。在这个过程中,摩擦力做负功所以机械能减少,A到C 和C到B摩擦力大小,位移都相等,所以机械能损失相同,D错;在这个过程中AC过程是重力分量加滑动摩擦力,C、B过程是重力分量减去滑动摩擦力,所以加速度不等,即速度的变化率不同,B对。
考查方向
解题思路
在判断速度大小时结合动能定理,在判断损失机械能时判断出重力之外其它力做功。
易错点
关键灵活运用牛顿第二定律与运动学公式及动能定理。注意方法的运用:逆向思维法、图象法等
知识点
扫码查看完整答案与解析