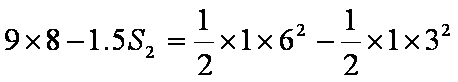- 机械能
- 共1183题
如图所示,粗糙水平地面AB与半径R=0.4m的光滑半圆轨道BCD相连接,且在同一竖直平面内,O是BCD的圆心,BOD在同一竖直线上。质量m=2kg的小物体在9N的水平恒力F的作用下,从A点由静止开始做匀加速直线运动。已知AB=5m,小物块与水平地面间的动摩擦因数为
求:
(1)小物块到达B点时速度的大小;
(2)小物块运动到D点时,轨道对小物块作用力的大小;
(3)小物块离开D点落到水平地面上的点与B点之间的距离。
正确答案
见解析。
解析
(1)从A到B,根据动能定理有 (

得 
(2)从B到D,根据机械能守恒定律有 
得 
在D点,根据牛顿运动定律有 
得 F= 
(3)由D点到落点小物块做平抛运动,在竖直方向有 
得 
水平面上落点与B点之间的距离为 x = vDt = 3×0.4 = 1.2m
知识点
如图所示,质量为m的小球A穿在绝缘杆上,细杆的倾角为α,小球A带正电,电荷量为q。在杆上B点处固定一个电荷量为Q的正电荷。将A由距B竖直高度为H处无初速释放,小球A下滑过程中电荷量不变,不计A与细杆间的摩擦,整个装置处于真空中,已知静电力常量k和重力加速度g,求:(1)A球刚释放时的加速度是多大?(2)当A球的动能最大时,A球与B点的距离?(3)若小球到达C点速度最大为v,求A、C两点的电势差UAC?(4)若小球到达D点的速度为0时,A、D两点间的电势差U0,则小球沿杆滑行的位移大小?
正确答案
见解析。
解析
(1)A球刚释放时,受到重力、沿细杆向上的库仑力和细杆的支持力,根据牛顿第二定律得:
得:
(2)到达平衡位置时,速度最大,根据平衡条件,有:
得:
(3)从A到C过程,只有重力和电场力做功,根据动能定理,有:
mgsinα•
将x代入,解得:
(4)从A到D过程,只有重力和电场力做功,设小球沿杆滑行的位移大小为x1,
根据动能定理,有:
mgsinα•x1-q•U0=0

知识点
一质量M=0.8kg的小物块,用长l=0.8m的细绳悬挂在天花板上,处于静止状态。一质量m=0.2kg的粘性小球以速度v0=10m/s水平射向物块,并与物块粘在一起,小球与物块相互作用时间极短可以忽略。不计空气阻力,重力加速度g取10m/s2。
求:
(1)小球粘在物块上的瞬间,小球和物块共同速度的大小;
(2)小球和物块摆动过程中,细绳拉力的最大值;
(3)小球和物块摆动过程中所能达到的最大高度。
正确答案
见解析。
解析
(1)因为小球与物块相互作用时间极短,所以小球和物块组成的系统动量守恒。
(2)小球和物块将以v共开始运动时,轻绳受到的拉力最大,设最大拉力为F,
F=15N
(3)小球和物块将以v共为初速度向右摆动,摆动过程中只有重力做功,所以机械能守恒;设它们所能达到的最大高度为h,根据机械能守恒定律:
h=0.2m
知识点
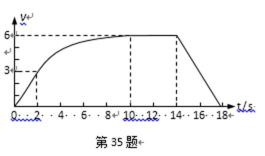
下图是一个遥控电动小车在水平直轨道上运动的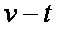

(1)小车所受到的阻力;
(2)小车匀速行驶阶段牵引力的功率;
(3)小车在加速运动过程中(指图像中0~10秒内)位移的大小。
正确答案
见解析
解析
(1)14~18s 内 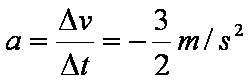

(2)匀速运动时,牵引力等于摩擦力 
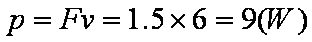
(3)0~3s 内匀加速运动 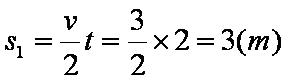
3s~10s 小车的功率 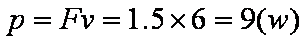
由动能定理可知
S2=39(m)
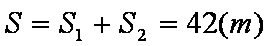
知识点
10.如图所示,粗糙、绝缘的直轨道OB固定在水平桌面上,B端与桌面边缘对齐,A是轨道上一点,过A点并垂直于轨道的竖直面右侧有大小E=1.5×106N/C,方向水平向右的匀强电场。带负电的小物体P电荷量是2.0×10-6C,质量m=0.25kg,与轨道间动摩擦因数μ=0.4,P从O点由静止开始向右运动,经过0.55s到达A点,到达B点时速度是5m/s,到达空间D点时速度与竖直方向的夹角为α,且tanα=1.2。P在整个运动过程中始终受到水平向右的某外力F作用,F大小与P的速率v的关系如表所示。P视为质点,电荷量保持不变,忽略空气阻力,取g=10 m/s2,求:
(1)小物体P从开始运动至速率为2m/s所用的时间;
(2)小物体P从A运动至D的过程,电场力做的功。
正确答案
(1)小物体P在速率从0至2m/s时,所受外力F1=2N,设其做匀变速直线运动的加速度为a1,经过时间△t1速度为v1,则
F1-μmg= ma1 ①
v1=a1△t1 ②
由①②式并代入数据得 △t1= 0.5s ③
说明:①②③式各2分。
(2)小物体P从速率为2m/s运动至A点,受外力F2=6N,设其做匀变速直线运动的加速度为a2则
F2-μmg= ma2 ④
设小物体P从速度v1经过△t2时间,在A点的速度为 v2,则
△t2=0.55s-△t1 ⑤
v2= v1+ a2△t2 ⑥
P从A点至B点,受外力F2=6N、电场力和滑动摩擦力的作用,使其做匀变速直线运动加速度为a3,电荷量为q,在B点的速度为v3,从A点至B点的位移为x1,则
F2-μmg-qE=ma3 ⑦


P 以速度v3滑出轨道右端B点,设水平方向受外力为 F3,电场力大小为FE,有
FE=F3 ⑨
F3与FE 大小相等方向相反,P水平方向所受合力为零,所以,P从点B点开始做初速度为v3的平抛运动。设P从B点运动至D点用时为△t3,水平位移为x2,由题意知

x2= v3△t3 ⑪
设小物体P从A点至D点电场力做功为W,则
W= -qE(x1+x2) ⑫
联立④⑧⑩~⑫式并代入数据得
W=-9.25J ⑬
解析
解析已在路上飞奔,马上就到!
知识点
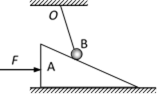
如图所示,一根细绳的上端系在O点,下端系一个重球B,放在粗糙的斜面体A上,现用水平推力F向右推斜面体使之在光滑水平面上向右匀速运动一段距离(细绳尚未到达平行于斜面的位置),在此过程中
正确答案
解析
略
知识点
如图,在电场强度为E、方向水平向右的匀强电场中,有两个质量均为m的小球A、B(可被视为质点),被固定在一根绝缘轻杆的两端,轻杆可绕与电场方向垂直的固定转动轴O无摩擦转动,小球A、B与轴O间的距离分别为



(1)轻杆转动到何位置时,小球A、B的速度达到最大;并分别求出A、B两球的最大动能。
(2)A、B两球从静止到获得最大速度的过程中系统的机械能和电势能如何变?变化了多少?
正确答案
见解析
解析
(1)当小球A、B的速度达到最大时,整个系统处于力矩平衡状态。
设此时轻杆与竖直方向夹角为
解得tan


当动能最大时,速度也最大,且vB=2vA ,EKB=4EKA 。
据动能定理,对A、B系统,杆从水平位置转到与竖直方向呈30°角位置时,A、B两球的动能达到最大值。
而
解得
(2)机械能减小,电势能增加,两者大小相等,
知识点
如图10甲所示,表面绝缘、倾角



(1)求线框受到的拉力F的大小;
(2)求匀强磁场的磁感应强度B的大小;
(3)已知线框向下运动通过磁场区域过程中的速度v随位移x的变化规律满足v=v0-
正确答案
见解析。
解析
(1)由v-t图象可知,在0~0.4s时间内线框做匀加速直线运动,进入磁场时的速度为v1=2.0m/s,所以在此过程中的加速度 a=
由牛顿第二定律
解得 F=1.5 N
(2)由v-t图象可知,线框进入磁场区域后以速度v1做匀速直线运动,
产生的感应电动势 E=BLv1
通过线框的电流 I=

线框所受安培力 F安=BIL=
对于线框匀速运动的过程,由力的平衡条件,有
解得 B=0.50T
(3)由v-t图象可知,线框进入磁场区域后做匀速直线运动,并以速度v1匀速穿出磁场,说明线框的宽度等于磁场的宽度 D=0.40m
线框ab边离开磁场后做匀减速直线运动,到达档板时的位移为s-D=0.15m
设线框与挡板碰撞前的速度为v2
由动能定理,有 
解得 v2=
线框碰档板后速度大小仍为v2,线框下滑过程中,由于重力沿斜面方向的分力与滑动摩擦力大小相等,即mgsinθ=μmgcosθ=0.50N,因此线框与挡板碰撞后向下做匀速运动,ab边刚进入磁场时的速度为v2=1.0 m/s;进入磁场后因为又受到安培力作用而减速,做加速度逐渐变小的减速运动,设线框全部离开磁场区域时的速度为v3
由v=v0-

因v3<0,说明线框在离开磁场前速度已经减为零,这时安培力消失,线框受力平衡,所以线框将静止在磁场中某位置。
线框向上运动通过磁场区域产生的焦耳热Q1=I2Rt=
线框向下运动进入磁场的过程中产生的焦耳热Q2=
所以Q= Q1+ Q2=0.45 J
知识点
如图所示,把质量为m、带电量为



正确答案
解析
略
知识点
如图所示,表面光滑的固定斜面顶端安装一个定滑轮,小物块A、B用轻绳连接并跨过滑轮(不计滑轮的质量和摩擦)。开始时A、B处于同一高度并恰好处于静止状态,现剪断轻绳后A自由下落,B沿斜面下滑,则在剪断轻绳到物块着地的过程中,两物块
正确答案
解析
略
知识点
扫码查看完整答案与解析