- 机械能
- 共1183题
如图12所示,用长为L的绝缘细线悬挂一带电小球,小球的质量为m、电荷量为q。现加一水平向左的匀强电场,平衡时小球静止于M点,细线与竖直方向成θ角。
(1)求匀强电场的电场强度E的大小;
(2)在某一时刻细线断裂,同时质量也为m的不带电的一小块橡皮泥,以水平向左的速度v0击中小球并与小球结合成一体,求击中后瞬间复合体的速度大小;
(3)若原小球离地高为h,求复合体落地过程中的水平位移大小。
正确答案
见解析。
解析
(1)小球受力平衡时有 

(2)橡皮泥撞击小球的过程中,水平方向动量守恒,
mv0=(m+ m)v
所以
(3)复合体水平方向的加速度为
复合体落地时间为
复合体在水平方向做匀加速直线运动,水平位移为x

知识点
如图所示,质量M=8kg的长木板放在光滑水平面上,在长木板的右端施加一水平恒力F=8N,当长木板向右运动速率达到v1=10m/s时,在其右端有一质量m=2kg的小物块(可视为质点)以水平向左的速率v2=2m/s滑上木板,物块与长木板间的动摩擦因数μ=0.2,小物块始终没离开长木板,
(1)经过多长时间小物块与长木板相对静止;
(2)上述过程中长木板对小物块摩擦力做的功.
正确答案
(1)8s
(2)192J
解析
(1)小物块的加速度为:a2=μg=2m/s2, 水平向右
长木板的加速度为:
令刚相对静止时他们的共同速度为v,以木板运动的方向为正方向
对小物块有:v=-v2+a2t
对木板有:v= v1+a1t
代入数据可解得:t=8s;v=14m/s
(2)长木板对小物块摩擦力做的功为
知识点
在孤立点电荷-Q的电场中,一质子在距离点电荷r0处若具有E0的动能,即能够恰好逃逸此电场的束缚。若规定无穷远处电势为零,用E表示该场中某点的场强大小,用φ表示场中某点的电势,用EP表示质子在场中所具有的电势能,用Ek表示质子在场中某点所具有的动能,用r表示该点距点电荷的距离,则下面选项所示的图像中,表示关系正确的是( )
正确答案
解析
略
知识点
如图所示,一根长为


正确答案

解析
略
知识点
2014年春晚中开心麻花团队打造的创意形体秀《魔幻三兄弟》给观众留下了很深的印象。该剧采用了 “斜躺” 的表演方式,三位演员躺在倾角为300的斜面上完成一系列动作,摄像机垂直于斜面拍摄,让观众产生演员在竖直墙面前表演的错觉。演员甲被演员乙和演员丙“竖直向上”抛出,到最高点后恰好悬停在“空中”。已知演员甲的质量m=60kg,该过程中观众看到演员甲上升的“高度”为0.8m。设演员甲和斜面间最大静摩擦力等于滑动摩擦力,重力加速度g=10m/s2,不计空气阻力。则该过程中,下列说法不正确的是:
正确答案
解析
略
知识点
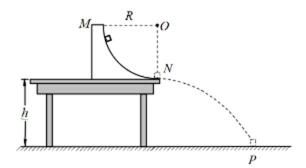
如图所示,半径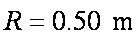
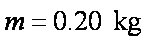
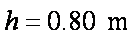

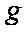

求:
(1)圆轨道上释放小物块的位置与桌面间的高度差;
(2)小物块经过
(3)小物块落地前瞬间的动量大小。
正确答案
见解析。
解析
(1)设圆轨道上释放小物块的位置与桌面间的高度差为H,小物块运动至N点过程中机械能守恒,则有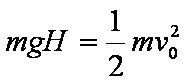
解得 H=0.45m
(2)设物块经过N点时所受支持力为F
根据牛顿第二定律有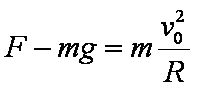
解得 F=5.6 N
(3)设物块做平抛运动的时间为t,小物块落地前竖直分速度为vy,
则 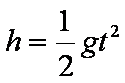
vy=gt
解得 vy=4.0m/s
小物块落地前速度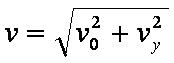
解得v=5.0m/s
动量p=mv
p=1.0kg·m/s
知识点
如图所示,一个质量为0。4 kg的小物块从高h=0。05m的坡面顶端由静止释放,滑到水平台上,滑行一段距离后,从边缘O点水平飞出,击中平台右下侧挡板上的P点,现以O为原点在竖直面内建立如图所示的平面直角坐标系,挡板的形状满足方程y=
正确答案
解析
略
知识点
如图所示,粗糙绝缘的水平面附近存在一个与x轴平行的水平电场,其在x轴上的电势φ与坐标x的关系用图中曲线表示,图中斜线为该曲线过点(0.15,3)的切线。现有一质量为0.20kg,电荷量为+2.0×10-8C的滑块P(可视为质点),从x=0.10m处由静止释放,其与水平面的动摩擦因数为0.02。设最大静摩擦力等于滑动摩擦力,取重力加速度g=10m/s2。问:
(1)滑块的加速度如何变化?请简要说明理由。
(2)滑块运动的最大速度为多大?
(3)滑块离出发点的最远距离为多大?
正确答案
见解析
解析
(1)滑块的加速度先向右变小后方向向左变大。
理由:斜率为电场强度,则可知沿x轴电场强度减小,方向为x轴正方向。
在x=0.15m处,
(2)滑块在0.15m处速度为最大。
由动能定律: 

(3)设最远在x 处,则由动能定理:


做图线交与x=0.23m处,即滑块离出发点的最远距离为0.13m。
知识点
如图所示,一质量为m的物块A与竖直轻弹簧的上端连接,弹簧的下端固定在地面上,一质量也为m的物块B放在A的上面,A、B处于静止状态。若A、B粘连在一起,用一竖直向上的拉力缓慢上提B,当拉力的大小为
(1)恒力F的大小;
(2)A与B分离时的速度大小
正确答案
见解析
解析
(1)设弹簧劲度系数为k,A、B静止时弹簧的压缩量为x,则:

A、B粘连在一起缓慢上移,以AB整体为研究对象,当拉力为

A、B不粘连,在恒力F作用下,恰好分离时,根据牛顿第二定律:

以B为研究对象,根据牛顿第二定律:

联立方程①②③④解得:
(2)A、B粘连在一起缓慢上移L,设弹簧弹力做功为W弹,根据动能定理;

在恒力F的作用下,设A、B分离时的速度为v,根据动能定理:
联立方程⑤⑥⑦解得:
说明:1.若通过计算得到

2.若将⑥⑦合写成
知识点
如图所示,水平轨道与竖直平面内的圆弧轨道平滑连接后固定在水平地面上,圆弧轨道B端的切线沿水平方向。质量m=1.0kg的滑块(可视为质点)在水平恒力F=10.0N的作用下,从A点由静止开始运动,当滑块运动的位移x=0.50m时撤去力F。已知A、B之间的距离x0=1.0m,滑块与水平轨道间的动摩擦因数μ=0.10,取g=10m/s2。求:
(1)在撤去力F时,滑块的速度大小;
(2)滑块通过B点时的动能;
(3)滑块通过B点后,能沿圆弧轨道上升的最大高度h=0.35m,求滑块沿圆弧轨道上升过程中克服摩擦力做的功。
正确答案
见解析。
解析
(1)滑动摩擦力 f=μmg
设滑块的加速度为a1,根据牛顿第二定律
F-μmg=ma1
解得 a1=9.0m/s2
设滑块运动位移为0.50m时的速度大小为v,根据运动学公式
v2=2a1x
解得 v =3.0m/s
(2)设滑块通过B点时的动能为EkB
从A到B运动过程中,依据动能定理有 W合=ΔEk
F x -fx0= EkB,
解得 EkB=4.0J
(3)设滑块沿圆弧轨道上升过程中克服摩擦力做功为Wf,根据动能定理
-mgh-Wf=0-EkB
解得 Wf=0.50J
知识点
扫码查看完整答案与解析