- 机械能
- 共1183题


正确答案
解析
拉力做功最小时,铁链重心到达水平面时的速度刚好为零,从开始拉铁链到铁链的重心到达水平面的过程中,运用动能定理得:
解得:
考查方向
功能关系; 动能定理
解题思路
要使把铁链沿斜面全部拉到水平面上,则需要把铁链的重心拉到水平面上,拉力做功最小时,重心到达水平面时的速度刚好为零,从开始拉铁链到铁链的重心到达水平面的过程中运用动能定理求解.
易错点
关键是知道拉力做功最小时,重心到达水平面时的速度刚好为零.
知识点
示波器是一种用途十分广泛的电子测量仪器。它能把肉眼看不见的电信号变换成看得见的图像,便于人们研究各种电现象的变化过程。如图所示,图①是示波管的原理图,它是由电子枪、加速电场、竖直偏转电极YY′、水平偏转电极XX′和荧光屏等组成。电子枪发射的电子打在荧光屏上将出现亮点。若亮点很快移动,由于视觉暂留,能在荧光屏上看到一条亮线。
14.质量为m电荷量为e的电子,从静止开始在加速电场中加速。加速电压为U1,竖直偏转电极YY′之间的电压为U2,YY′之间的距离为d,电极极板的长和宽均为L,水平偏转电极XX′两极板间电压为0。若电子被加速后沿垂直于偏转电场的方向射入电场,并最终能打到荧光屏上。
① 电子进入偏转电场时的速度大小;
② 电子打到荧光屏上时的动能大小;
如果只在偏转电极XX上加上如图②所示的电压,试在答题卡的图①上画出在荧光屏所能观察到的亮线的形状。
16.如果在偏转电极YY′加上Uy=Umsinωt的电压,同时在偏转电极XX′上加上图②所示的电压,试在答题卡的图

正确答案
①
②电子打到荧光屏上时的动能为:
解析
①设电子经电子枪加速后进入偏转电极YY′的速度为v0,
则有:
②偏转电极的电压为U2,板间距离为d,板长为L,
则有:
a=

即电子在电场中的偏转距离为:y=
电子打到荧光屏上时的动能为:
考查方向
带电粒子在匀强电场中的运动.
解题思路
由动能定理求的在加速电场中获得的速度,由运动学公式求的在偏转电场中的偏移量
易错点
考查对示波器工作原理的理解,其基本原理是电场的加速和偏转,根据偏转距离与偏转电压的关系,分析荧光屏上光斑的变化.
正确答案
解析
考查方向
带电粒子在匀强电场中的运动.
解题思路
通过交流电压的变化,通过运动分析即可画出荧光屏上的图形
易错点
考查对示波器工作原理的理解,其基本原理是电场的加速和偏转,根据偏转距离与偏转电压的关系,分析荧光屏上光斑的变化
正确答案
解析
考查方向
带电粒子在匀强电场中的运动.
解题思路
通过交流电压的变化,通过运动分析即可画出荧光屏上的图形
易错点
考查对示波器工作原理的理解,其基本原理是电场的加速和偏转,根据偏转距离与偏转电压的关系,分析荧光屏上光斑的变化
应纳入政府资本预算支出范围之内的项目有( )。
A.国家政权建设的政府日常行政经费支出
B.各项事业费和社会保障支出
C.政府对国营企业的投资
D.政府对公共工程项目的投资
E.政府贷款及偿还国债支出
正确答案
C,D,E
解析
[解析] AB两项应纳入政府经常预算支出的范畴,CDE三项属于政府资本预算支出的范畴。政府的资本预算支出主要包括政府的各项资本性支出,如政府对国营企业的投资、对公共工程项目的投资、战略物资储备、政府贷款以及偿还国债等支出;政府的资本预算收入主要包括国有资产经营收益、资产处置收入、债务收入、经常结算结余转入等。故本题答案为CDE。
33.静电场方向平行于x轴,其电势φ随x的分布如图所示,图中φ0和d为已知量。一个带负电的粒子在电场中以x=0为中心,沿x轴方向做周期性运动.已知该粒子质量为m、电量为-q,其动能与电势能之和为-A(0<A<qφ0)。忽略重力。求:
(1)粒子所受电场力的大小;
(2)粒子的运动区间;
(3)粒子从左侧最远点运动到中心点O处的时间。
正确答案
(1)
(2)-d(1-

(3)(2n+1)
解析
(1)由图可知,0与d(或-d)两点间的电势差为φ0,所以电场强度的大小:E=
电场力的大小:F=qE=
(2)设粒子在[—x,x]区间内运动,速率为v,由动能定理有: 
由图可知:
由①②得:
因动能非负,有:
得:
即:
粒子运动区间:-d(1-

(3)考虑粒子从-x0处开始运动的四分之一周期
根据牛顿第二定律,粒子的加速度:
由匀加速直线运动: 
将④⑤代入,得:
粒子从左侧最远端运动到O点所用时间:
tn=(2n+1)
考查方向
解题思路
见解析
易错点
题给图线的斜率代表了电场强度分析不清、周期性带来的多解性
知识点
14.如图,在水平轨道右侧固定半径为R的竖直圆槽形光滑轨道,水平轨道的PQ段铺设特殊材料,调节其初始长度为l,水平轨道左侧有一轻质弹簧左端固定,弹簧处于自然伸长状态。可视为质点的小物块从轨道右侧A点以初速度v0冲上轨道,通过圆形轨道、水平轨道后压缩弹簧,并被弹簧以原速率弹回。已知R=0.4 m,l=2.5m,v0=6m/s,物块质量m=1kg,与PQ段间的动摩擦因数μ=0.4,轨道其它部分摩擦不计。取g=10m/s2.
求:
(1)物块第一次经过圆轨道最高点B时对轨道的压力;
(2)物块仍以v0从右侧冲上轨道,调节PQ段的长度l,当l长度是多少时,物块恰能不脱离轨道返回A点继续向右运动.
正确答案
(1)、
(2)、L=1m
解析
解:(1)对物块,首次从A到B,有
在B点,有:
解得:
根据牛顿第三定律,小球对轨道的压力大小为40N,方向竖直向上。
(2)对物块,从A点到第二次到达B点:
在B点,有:
解得:L=1m
考查方向
解题思路
由于是单个物体做多过程、曲线运动的问题,所以要用动能定理列方程求解
易错点
(2)问中不脱离轨道返回A点的理解:只要物体能返回最高的B就能回到A点,所以 从A点到第二次到达B点:
在B点,有:
知识点
19.相距L=1 m的足够长金属导轨竖直放置,质量为m1=1 kg的金属棒ab和质量为m2=0.02 kg的金属棒cd均通过棒两端的套环水平地套在金属导轨上,如图所示,虚线上方磁场的磁感应强度B=1T,方向垂直纸

⑴当时间t=2s时拉力F的大小;
⑵当cd棒通过2C的电量时,其产生的热量为2.5J,则外力F需要做功为多少;
⑶判断cd棒将做怎样的运动,求出cd棒达到最大速度所需的时间t0,
正确答案
(1)F=11.5N
(2)WF=93J
(3)见解析
解析
⑴ 



⑵ 





⑶ cd棒先做加速度逐渐减小的加速运动,当cd棒所受重力与滑动摩擦力相等时,速度达到最大;后做加速度逐渐增大的减速运动,最后停止运动.当cd棒速度达到最大时,有:


对abcd回路,有:

又
fcd随时间变化的图象如图所示。
考查方向
解题思路
(1)由E=BLv、 
(2)由



(3)分析cd棒的运动情况:cd棒先做加速度逐渐减小的加速运动,当cd棒所受重力与滑动摩擦力相等时,速度达到最大;然后做加速度逐渐增大的减速运动,最后停止运动.
cd棒达到最大速度时重力与摩擦力平衡,而cd棒对导轨的压力等于安培力,可求出电路中的电流,再由E=BLv、欧姆定律求出最大速度.
易错点
本题中cd棒先受到滑动摩擦,后受到静摩擦,发生了突变,要仔细耐心分析这个动态变化过程.滑动摩擦力与安培力有关,呈现线性增大.
知识点
如图所示,一轻弹簧一端与竖直墙壁相连,另一端与放在光滑水平面上的长木板左端接触,轻弹簧处于原长,长木板的质量为M,一物块以初速度






29.滑块上长木板的一瞬间,长木板的加速度大小;
30.长木板向左运动的最大速度;
31.长木板的长度
正确答案
解析
物块滑上长木板时,长木板受到的合外力等于滑块对长木板的摩擦力,由牛顿第二定律得:μmg=Ma
解得,长木板的加速度
考查方向
牛顿第二定律
解题思路
物块在长木板滑动时,长木板受到的合外力等于滑块对长木板的摩擦力,由牛顿第二定律求出长木板的加速度.
易错点
滑块上长木板的一瞬间,弹簧还没有被压缩,此时长木板受到的合力为滑块对长木板的摩擦力.
正确答案
解析
当长木板向左运动的最大速度时,弹簧的弹力等于滑块对长木板的摩擦力,即 kx=μmg,解得
长木板从开始运动到速度最大的过程,设最大速度为v,由动能定理得:
解得:
考查方向
动能定理;牛顿运动定律的综合应用
解题思路
当长木板向左运动的最大速度时,弹簧的弹力等于滑块对长木板的摩擦力,由胡克定律求弹簧的压缩量.长木板从开始运动到速度最大的过程,运用动能定理求最大速度.
易错点
关键分析清楚长木板的运动情况,当长木板的加速度为0时,长木板速度最大.
正确答案
解析
当弹簧的压缩量达到最大时,木板的速度为零,木块的速度也为零,设长木板的长度为L,根据能量守恒定律得:
解得:
考查方向
功能关系
解题思路
当弹簧的压缩量达到最大时,木板的速度为零,木块的速度也为零,根据能量守恒定律求长木板的长度.
易错点
抓住弹簧的压缩量达到最大时,木板和木块的速度均为零,运用能量守恒定律列式求解.
11.嘉年华上有一种回力球游戏,如图所示,A、B分别为一固定在竖直平面内的光滑半圆形轨道的最高点和最低点,B点距水平地面的高度为h,某人在水平地面C点处以某一初速度抛出一个质量为m的小球,小球恰好水平进入半圆轨道内侧的最低点B,并恰好能过最高点A后水平抛出,又恰好回到C点抛球人手中。若不计空气阻力,已知当地重力加速度为g,求:
(1)小球刚进入半圆形轨道最低点B时轨道对小球的支持力;
(2)半圆形轨道的半径;
(3)小球抛出时的初速度大小。
正确答案
(1)6mg
(2)2h
(3)
解析
(1)设半圆形轨道的半径为R,小球经过A、B两点的速度分别为vA、vB,在B点轨道对小球的支持力为N。小球恰好通过最高点,则在A点处,仅由重力提供向心力:mg=
取小球为研究对象,从B到A的过程中,由动能定理有-mg2R=
在B点处,由牛顿第二定律有:N-mg=
(2)小球从A点飞出后做平抛运动,则:h=

(3)设小球抛出时的速度大小为v0,由C到B的过程中,由动能定理有:-mgh=
解得:v0=
考查方向
解题思路
见解析
易错点
竖直平面内圆周运动的临界条件
知识点
15.如图所示,一个光滑绝缘细椭圆环固定放置在水平面上,其长轴AC的延长线两侧固定有两个等量异号点电荷,电量绝对值为Q,两者连线的中点O恰为椭圆的中心,BD为椭圆的短轴。一带电量为q的小球套在环上(q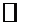
正确答案
解析
A选项,由于vC < vA,根据动能定理,可知从A到C动能减小,电势能增加,电场力做负功,小球带负电,故错误。
B选项,根据正负电荷周围电场强度的分布特点,可知电场强度,沿两电荷连线先减小后增大,连线的中点电场强度最小,故小球在A点受到的电场力大于在B点受到的电场力,故错误。
C选项,如图所示异号点电荷的等势面分布,可知B、D两点电势相等,小球从B点到D点电场力不做功,动能不变,故C选项正确。
D选项,小球从A到C过程中动能减小,电势能增加,从C到A动能增加,电势能减小,故C点电势能最大,故错误。
考查方向
1、考查正负电荷在真空中,电场、电势分布的对称性。
2、考查点电荷间的静电引力公式:
3、电场能与动能之间的相互转化,功能关系,动能定理,电场力做功。
解题思路
A选项,由于vC < vA,根据动能定理,可知从A到C动能减小,电势能增加,电场力做负功,小球带负电,故错误。
B选项,根据正负电荷周围电场强度的分布特点,可知电场强度,沿两电荷连线先减小后增大,连线的中点电场强度最小,故小球在A点受到的电场力大于在B点受到的电场力,故错误。
C选项,如图所示异号点电荷的等势面分布,可知B、D两点电势相等,小球从B点到D点电场力不做功,动能不变,故C选项正确。
D选项,小球从A到C过程中动能减小,电势能增加,从C到A动能增加,电势能减小,故C点电势能最大,故错误。
易错点
对正负电荷在真空中,电场、电势的对称性分布理解不到位。
知识点
如图所示,一倾斜传送带与水平方向夹角37°。传送物体。已知传送带总长度LAB =9.75m,以恒定速度v=2.0m/s顺时针转动。在距传送带底端A点9m的C点上方存在水平向左的匀强电场,电场强度50000N/C,现将一个质量m=2.0kg,电量
15.若不加电场,物块由底端A放上到相对传送带静止,物块相对传送带的位移S相;
16.加电场后,物块由底端A传送到顶端B所用时间t;
17.加电场后,将物块由底端A传送到顶端B过程中,传送带克服物块摩擦力做功W。
正确答案
5m;
解析
(1)对物体: μmgcosθ-mgsinθ=ma1 ----------1分
加速过程: V=a1t1 ----------1分
物块:S1=a1t12 /2 
传送带:S2=Vt1 ----------1分
相对位移:S相=S2-S1
解得a1=0.4m/s2 t1=5s S1=5m S2=10m S相=5m ----------1分
考查方向
解题思路
首先通过运动学特征分析物体的加速度,通过对物体受力分析求加速度,利用功能关系求克服摩擦力做功。
易错点
牛顿第二定律在求加速度时要注意将电场力计算进去
正确答案
7.5s;
解析
(2)加电场后:
匀速运动过程中:t2=(LAC-s1)/v ----------1分
CB段:mgsinθ+Eqcosθ-μ(mgcosθ-Eqsinθ)=ma2 ----------2分
减速过程中:sCB=vt3- a2t32/2 ----------1分
V’=v-a2t3 ----------1分
解得:t2=2s a2=2m/s2向下 t3=0.5s v’=1m/s
所以t总=t1+t2+t3=7.5s ----------2分
考查方向
解题思路
首先通过运动学特征分析物体的加速度,通过对物体受力分析求加速度,利用功能关系求克服摩擦力做功。
易错点
牛顿第二定律在求加速度时要注意将电场力计算进去
正确答案
187J
解析
(3)减速过程中物块相对传送带位移S’相=vt3-sCB 
A-C 摩擦生热Q1=μmgcosθS相 ----------1分
C-B 摩擦生热Q2=μmgcosθS’相 ----------1分
解得:S’相=0.25m, Q1=64J Q2=2.75J 总摩擦生热Q= Q1+ Q2
A— B功能关系得:
W-EqsCBcosθ=mgLABsinθ+mv2/2+Q ---------2分
得:W=187J
所以传送带克服物块摩擦力做功为187J。 ----------1分
考查方向
解题思路
首先通过运动学特征分析物体的加速度,通过对物体受力分析求加速度,利用功能关系求克服摩擦力做功。
易错点
牛顿第二定律在求加速度时要注意将电场力计算进去
扫码查看完整答案与解析