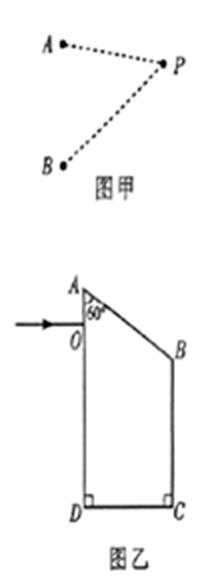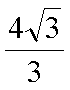- 波长、频率和波速的关系
- 共149题
如图,简谐横波在t时刻的波形如实线所示,经过Δt=3s,其波形如虚线所示。己知图中x1与x2相距lm,波的周期为T,且2T<Δt<4T 。则可能的最小波速为____________m/s,最小周期为____________s。
正确答案
5;
7/9
解析
若波向正x方向传播,




若波向正x方向传播,





知识点
(1)如图甲所示,在某一均匀介质中,A、B是振动情况完全相同的两个波源,其简谐运动表达式均为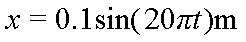
①求简谐横波的波长。
②P点的振动 (填“加强”或“减弱”)。
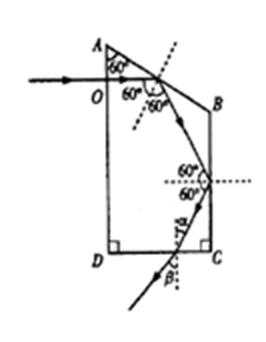
(2)如图乙所示,ABCD是一直角梯形棱镜的横截面,位于截面所在平面内的一束光线由O点垂直AD边射入。已知棱镜的折射率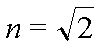
①求光线第一次射出棱镜时,出射光线的方向。
②第一次的出射点距C cm。
正确答案
见解析。
解析
(1)①设简谐波的波速为v,波长为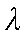
T=0.1s
由波速公式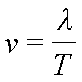
打入数据得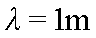
②加强
(2)①设发生全反射的临界角为C,由折射定律得
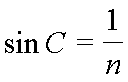
代入数据得
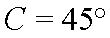
光路图如图所示,
由几何关系可知光线在AB边和BC边的入射角均为60°,均发生全反射。设光线在CD边的入射角为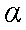
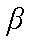


代入数据得 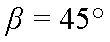
②
知识点
在O点有一波源,t=0时刻开始向上振动,形成向右传播的一列横波。t1=4s时,距离O点为3m的A点第一次达到波峰;t2=7s时,距离O点为4m的B点第一次达到波谷。则以下说法正确的是()
正确答案
解析


解得
波长
振动从O传到距离O点为1m的质点所需时间
知识点
(1)一列简谐横波沿直线传播,某时刻该列波上正好经过平衡位置的两质点相距6m,且这两质点间的波峰只有一个,则该简谐横波可能的波长为
A.4 m、6 m和8 m
B.6 m、8 m和12 m
C.4 m、6 m和12 m
D.4 m、8 m和12 m
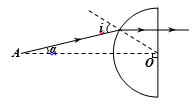
(2)利用半球柱形玻璃,可减小激光光束的发散程度。在题图所示的光路中,A为激光的出射点,O为半球柱形玻璃横截面的圆心,AO过半圆顶点。若某条从A点发出的与AO成α角的光线,以入射角i入射到半圆弧上,出射光线平行于AO,求此玻璃的折射率。
正确答案
(1)C
(2)
解析
(1)符合题意的波形有三种,如图所示:
则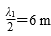
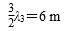
(2)如图所示,由几何关系知: i=α+r 所以r=i-α
所以此玻璃的折射率
知识点
(1)(6分)如图所示是一列简谐波在t=0时的波形图象,波速为v=10 m/s,此时波恰传到I点,下列说法中正确的是________(填入正确选项前的字母,选对1个给3分,选对2个给4分,选对3个给6分;每选错一个扣3分,最低得分为0分)。
A. 此列波的周期为T=0.4 s
B. 质点B、F在振动过程中位移总是相等
C. 质点I的起振方向沿y轴负方向
D. 当t=5.1 s时,x=10 m的质点处于平衡位置处
E. 质点A、C、E、G、I在振动过程中位移总是相同
(2)(9分)桌面上有一玻璃圆锥,圆锥的轴(图中的虚线)与桌面垂直,过轴线的截面为等边三角形,此三角形的边长为L,如图所示,有一半径为

①光在玻璃圆锥中的传播速度;
②光束在桌面上形成光斑的面积。
正确答案
(1)ABC
(2)①1.73×108 m/s;②
解析
(1)从图象中可以看出,波长为λ=4 m,周期T=
(2)①由n=
解得:v=1.73×108 m/s(1分)
②光路如图,
由几何知识可得,
光束边缘光线在侧面上的入射角θ1=60°
由n=
得折射角θ2=30°(1分)
又因为OA=
△OBE为等边三角形,所以BE=L-OA=
光斑半径R=
所以光斑面积S=
知识点
(1)图(a)为一列简谐横波在t=2s时的波形图,图(b)为媒质中平衡位置在x=1.5m处的质点的振动图像,P是平衡位置为x=2m的质点。下列说法正确的是 。
A,波速为0.5m/s
B,波的传播方向向右
C,0~2s时间内,P运动的路程为8cm
D,0~2s时间内,P向y轴正方向运动
E.当t=7s时,P恰好回到平衡位置
(2)一个半圆柱形玻璃砖,其横截面是半径为R的半圆,AB为半圆的直径,O为圆心,如图所示。玻璃的折射率为n=
(i)一束平行光垂直射向玻璃砖的下表面,若光线到达上表面后,都能从该表面射出,则入射光束在AB上的最大宽度为多少?
(ii)一细数光线在O点左侧与O相距
正确答案
(1) ACE
(2)
(i)解:在O点左侧,设从E点射入的光线进入玻璃砖后在上表面的入射角恰好等于全反射的临界角

由几何关系有

由对称性可知,若光线都能从上表面射出,光束的宽度最大为

联立①②③式,代入已知数据得

(ii)
设光线在距O点



光线在玻璃砖内会发生三次全反射,最后由G点射出,如图。由反射定律和几何关系得

射到G点的光有一部分被反射,沿原路返回到达C点射出。
解析
略
知识点
(1)一列简谐横波沿直线传播。以波源O由平衡位置开始振动为计时零点,质点A的振动图像如图所示,已知O.A的平衡位置相距0.9m.以下判断正确的是________。(双选,填正确答案标号)
a.波长为1.2m
b.波源起振方向沿y轴正方向
c.波速大小为0.4m/s
d.质点A的动能在
(2)如图,三角形ABC为某透明介质的横截面,O为BC边的中点,位于截面所在平面内的束光线自O以角入射,第一次到达AB边恰好发生全反射。已知

(ⅰ)入射角i;
(ⅱ)从入射到发生第一次全反射手忙脚乱的时间(设光在真空中的速度为c,可能用到

正确答案
(1)ab
(2)解:
(ⅰ)根据全反射定律可知,光线在AB面上P点的入射角等于临界角C,由折射定律得:

代入数据得

设光线在BC面上的折射角为r,由几何关系得

由折射定律得

联立③④式,代入数据得

(ⅱ)在

设所用时间为t,光线在介质中的速度为v,得


联立⑥⑦⑧式,代入数据得

解析
略。
知识点
一简谐横波以4m/s的波速沿x轴正方向传播。已知t=0时的波形如图所示,则
正确答案
解析
解析:由波的图像可知半个波长是2m,波长是4m,周期是





知识点
(1)如图所示,一列简谐波沿x轴传播,实线为t1=0时的波形图,此时P质点向y轴负方向运动,虚线为t2=0.01s时的波形图。已知周期T >0.01s。
①波沿x轴_______(填“正”或“负”)方向传播。
②求波速。
(2)如图所示,扇形AOB为透明柱状介质的横截面,圆心角∠AOB=60°。一束平行于角平分线OM的单色光由OA射入介质,经OA折射的光线恰平行于OB。
①求介质的折射率。
②折射光线中恰好射到M点的光线_______(填“能”或“不能”)发生全反射。
正确答案
(1)①正;②100m/s
(2)①
解析
(1)①t1=0时,P质点向y轴负方向运动,由波的形成与传播知识可以判断波沿x轴正向传播。
②由题意知 

联立①②式代入数据求得
(2)①依题意作出光路图,如图所示。由几何知识知入谢角i=600,折射角γ=300。根据折射定律

②,
而

知识点
3.图甲为一列简谐横波在某一时刻的波形图,a、b两质点的横坐标分别为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析