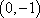- 椭圆的几何性质
- 共137题
直线y＝kx＋m(m≠0)与椭圆W：
（1）当点B的坐标为(0,1)，且四边形OABC为菱形时，求AC的长；
（2）当点B在W上且不是W的顶点时，证明：四边形OABC不可能为菱形。
正确答案
见解析
解析
（1）因为四边形OABC为菱形，所以AC与OB相互垂直平分。
所以可设A
所以|AC|＝
（2）假设四边形OABC为菱形。
因为点B不是W的顶点，且AC⊥OB，所以k≠0.
由
设A(x1，y1)，C(x2，y2)，
则
所以AC的中点为M
因为M为AC和OB的交点，且m≠0，k≠0，所以直线OB的斜率为
因为k·
所以四边形OABC不是菱形，与假设矛盾。
所以当点B不是W的顶点时，四边形OABC不可能是菱形。
知识点
设椭圆C：
A
B
C
D
正确答案
解析
如图所示，在Rt△PF1F2中，|F1F2|＝2c，
设|PF2|＝x，则|PF1|＝2x，
由tan 30°＝
而由椭圆定义得，|PF1|＋|PF2|＝2a＝3x，
∴
知识点
如图，中心均为原点O的双曲线与椭圆有公共焦点，M，N是双曲线的两顶点，若M，O，N将椭圆长轴四等分，则双曲线与椭圆的离心率的比值是( )
A3
B2
C
D
正确答案
解析
由题意可知椭圆的长轴长2a1是双曲线实轴长2a2的2倍，即a1＝2a2，而椭圆与双曲线有相同的焦点。
故离心率之比为
知识点
如图，F1，F2是椭圆C1：
A
B
C
D
正确答案
解析
椭圆C1中，|AF1|＋|AF2|＝2a＝4，|F1F2|＝2c＝
知识点
已知点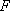
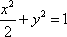
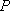
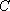
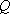
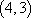
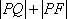
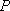
正确答案
解析
略
知识点
扫码查看完整答案与解析