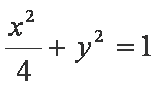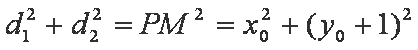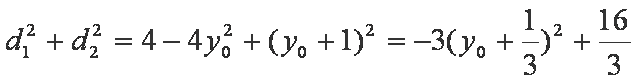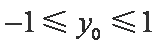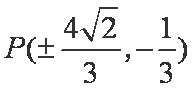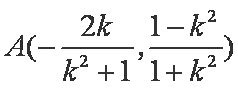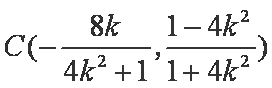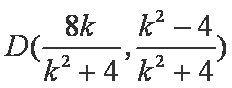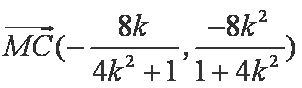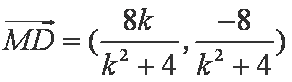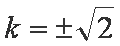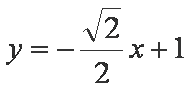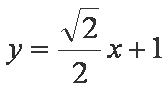- 椭圆的几何性质
- 共137题
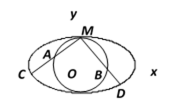
如图,圆
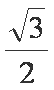
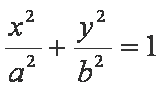

(1)求椭圆的方程;
(2)过点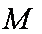
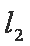
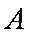

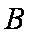
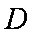
(ⅰ)若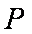
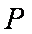
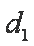
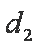
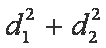
(ⅱ)若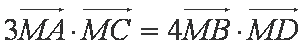
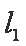
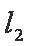
正确答案
见解析。
解析
(1)由题意: 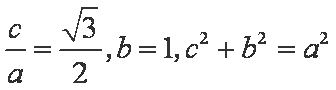
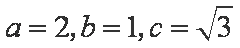
椭圆的方程为
(2)(ⅰ)设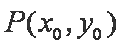
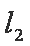
因为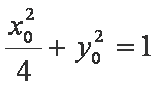
因为
所以当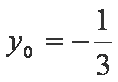
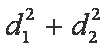
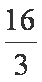
此时点
(ⅱ)设
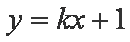
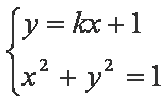
由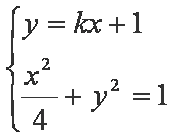
同理可得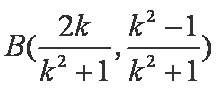
所以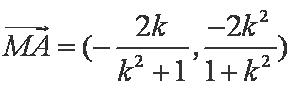
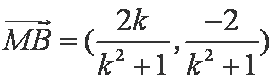
由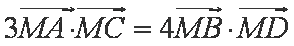
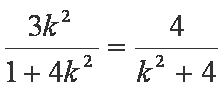
所以
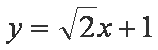
或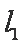
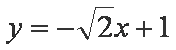
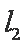
知识点
已知椭圆C的中心在坐标原点,焦点在x轴上,离心率为

(1)求椭圆C的标准方程;
(2)若A、B是椭圆C上关x轴对称的任意两点,设P(﹣4,0),连接PA交椭圆C于另一点E,求证:直线BE与x轴相交于定点M;
(3)设O为坐标原点,在(2)的条件下,过点M的直线交椭圆C于S、T两点,求

正确答案
见解析。
解析
(1)由抛物线x2=4

设椭圆方程为
由题意可得

∴椭圆的方程为
(2)证明:由题意可知直线PA的斜率存在,设直线PA的方程为y=k(x+4),
联立
设点A(x1,y1),E(x2,y2),则B(x1,﹣y1)。
直线BE的方程为
令y=0,则
把y1=k(x1+4),y2=k(x2+4)代入上式并整理得
由①得


∴直线BE与x轴相交于定点M(﹣1,0)。
(3)当过点M的直线斜率存在时,设直线ST的方程为y=m(x+1),且S(x3,y3),T(x4,y4)在椭圆C上,
联立
则△=(8m2)2﹣4(4m2+3)(4m2﹣12)=144(m2+1)>0。
∴

∴

∴


由m2≥0得
当过点M的直线斜率不存在时,直线ST的方程为x=﹣1,

此时,
∴


知识点
如图,设椭圆




(1)求椭圆
(2)已知





正确答案
见解析
解析
(1)
由

因为

(2)由(1)可知

解得
由


即点

因为圆心

故该圆与直线


知识点
10.已知函数
正确答案
解析
函数y=f(x)是一个非奇非偶函数,图象不关于原点对称,故排除选项A、C,又当x>0时,函数值大于0恒成立,故排除D,故选 B。
知识点
8.已知








正确答案
解析
有对称性不妨设





知识点
扫码查看完整答案与解析