- 弹性碰撞和非弹性碰撞
- 共16题
22.从22A 22B两题中选择一体作答。
(22A)两小孩在冰面上乘坐“碰碰车”相向运动。A车总质量为50kg,以2m/s的速度向右运动;B车总质量为70kg,以3m/s的速度向左运动。碰撞后,A以1.5m/s的速度向左运动,则B的速度大小为________m/s,方向向________(选填“左”或“右”)。
(22B)两靠得较近的天体组成的系统称为双星,它们以两者连线上某点为圆心做匀速圆周运动,因而不至于由于引力作用而吸引在一起。设两天体的质量分别为m1和m2,则它们的轨道半径之比Rm1:Rm2=________;速度之比vm1:vm2=________。
正确答案
(22.A)0.5;左 (22.B)
解析
22A对两小孩由动量守恒定律得。22B本题属于双星问题,抓住双星的周期、角速度、引力相同,有F=mRω2得R与ω成反比,速度与R成正比
考查方向
解题思路
22A设正方向,列动量守恒矢量方程;22B双星问题,抓住双星的三个相同分析
易错点
方向性,计算
知识点
某同学用一个光滑的半圆形轨道和若干个大小相等、可视为质点的小球做了三个有趣的实验,轨道固定在竖直平面内,且两端同高。第一次,他将一个小球从离轨道最低点的竖直高度h处由静止沿轨道下滑(h远小于轨道半径),用秒表测得小球在轨道底部做往复运动的周期为T;第二次,他将小球A放在轨道的最低点,使另一个小球B从轨道最高点由静止沿轨道滑下并与底部的小球碰撞,结果小球B返回到原来高度的1/4,小球A也上滑到同样的高度;第三次,用三个质量之比为m1:m2:m3=5:3:2的小球做实验,如图所示,先将球m2和m3放在轨道的最低点,球m1从某一高度由静止沿轨道下滑,它们碰后上升的最大高度分别为h1、h2和h3,不考虑之后的碰撞。设实验中小球间的碰撞均无能量损失。重力加速度为g。
求:
(1)半圆形轨道的半径R;
(2)第二次实验中两小球的质量之比mA:mB;
(3)第三次实验中三个小球上升的最大高度之比h1:h2:h3。
正确答案
见解析。
解析
(1)第一次实验中,小球的运动可以看做摆长为R的单摆,根据单摆周期公式有:
所以 
(2)第二次实验中,球B从高为R处释放,设球B与球A碰撞前瞬间的速度大小为vB,碰撞后瞬间它们速度的大小分别为

所以 
又根据动量守恒定律有
所以 
(3)根据题意设球1、2、3的质量分别为5m、3m和2m。设球1与球2碰撞前后的速度分别为v1、


球1与球2碰撞过程中动量守恒,且机械能守恒,则有
解得
球2与球3碰撞过程中动量守恒,且机械能守恒,则有
解得:
在三个小球的上升过程中,根据机械能守恒定律有
解得
知识点
如图所示,两物体A、B分别与一竖直放置的轻质弹簧的两端相连接,B物体在水平地面上,A、B均处于静止状态。从A物体正上方与A相距H处由静止释放一小物体C。C与A相碰后立即粘在一起向下运动,以后不再分开。弹簧始终处于弹性限度内。用ΔE表示C与A碰撞过程中损失的机械能,用F表示C与A一起下落过程中地面对B的最大支持力。若减小C物体释放时与A物体间的距离H,其他条件不变,则
正确答案
解析
略
知识点
(1)如图所示是研究光电效应的实验装置,某同学进行了如下操作:
①用频率为ν1的光照射光电管,此时电流表中有电流。调节滑动变阻器,将触头P向 端滑动(选填“a”或“b”),使微安表示数恰好变为零,记下电压表示数U1。
②用频率为ν2的光照射光电管,重复①中的步骤,记下电压表示数U2。
已知电子的电量为e,由上述实验可知,普朗克常量h= (用上述已知量和测量量表示)。
(2)(9分)如图所示,光滑的水平面上静止着半径相同的三个小球A、B、C,其中小球A、C的质量分别为mA=m、mC=4m。现使A以初速
正确答案
(1)a (3分) 
(2)解:
以碰撞前A球的速度方向为正,A球与B球发生弹性碰撞,设碰撞后的速度分别为



解得 
B球与C球发生弹性碰撞,设碰撞后的速度分别为


解得 
故C球碰撞后的速度
由数学关系解得
解析
略
知识点
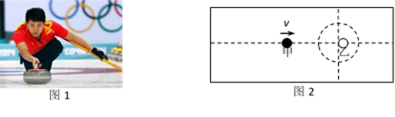
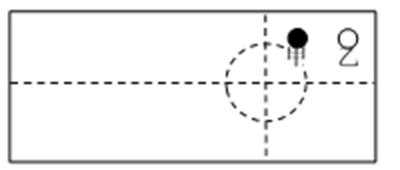
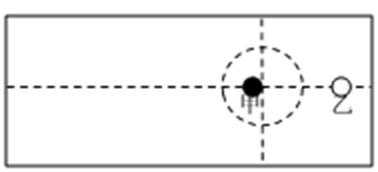
冰壶运动深受观众喜爱,图1为2014年2月第22届索契冬奥会上中国队员投掷冰壶的镜头。在某次投掷中,冰壶甲运动一段时间后与对方静止的冰壶乙发生正碰,如图2。若两冰壶质量相等,则碰后两冰壶最终停止的位置,可能是选项中的哪幅图
正确答案
解析
略
知识点
扫码查看完整答案与解析