- 平抛运动
- 共223题
如图所示,长为L、内壁光滑的直管与水平地面成30°角固定放置。将一质量为m的小球固定在管底,用一轻质光滑细线将小球与质量为M=km的小物块相连,小物块悬挂于管口。现将小球释放,一段时间后,小物块落地静止不动,小球继续向上运动,通过管口的转向装置后做平抛运动,小球在转向过程中速率不变。(重力加速度为g)
(1)求小物块下落过程中的加速度大小;
(2)求小球从管口抛出时的速度大小;
(3)试证明小球平抛运动的水平位移总小于
正确答案
(1) 
(2)
(3)见解析
解析
(1)设细线中的张力为T,根据牛顿第二定律
且
解得:
(2)设M落地时的速度大小为v,m射出管口时速度大小为v0,M落地后m的加速度为a0。
根据牛顿第二定律
匀变速直线运动
解得: 
(3)平抛运动
解得
因为

知识点
如图,质量为M、长为L、高为h的矩形滑块置于水平地面上,滑块与地面间动摩擦因数为μ;滑块上表面光滑,其右端放置一个质量为m的小球。用水平外力击打滑块左端,使其在极短时间内获得向右的速度v0,经过一段时间后小球落地。求小球落地时距滑块左端的水平距离。
正确答案
见解析。
解析
在m从右边缘至左边缘时M的加速度
设此时M的速度为v1,所以可得
在m离开M做自由落体运动时,M的加速度
讨论
(1)当m落地使M已停止,那么

(2)当m落地使M未停止,那么


知识点
如图所示,四分之一圆轨道OA与水平轨道AB相切,它们与另一水平轨道CD在同一竖直面内,圆轨道OA的半径R=0.45m,水平轨道AB长S1=3m, OA与AB均光滑。一滑块从O点由静止释放,当滑块经过A点时,静止在CD上的小车在F=1.6N的水平恒力作用下启动,运动一段时间后撤去力F。当小车在CD上运动了S2=3.28m时速度υ=2.4m/s,此时滑块恰好落入小车中。已知小车质量M=0.2kg,与CD间的动摩擦因数μ=0.4。(取g=10m/s2)求
(1)恒力F的作用时间t。
(2)AB与CD的高度差h。
正确答案
(1)1s (2)0.8m
解析
(1)设小车在恒力F作用下的位移为l,由动能定理得
F l − μMg s2 =
由牛顿第二定律得
F − μMg = Ma
由运动学公式得
l = 
联立以上三式,带入数据得
a = 4m/s2 t = 
(2)滑块由O滑至A的过程中机械能守恒,即
mgR = 
AB段运动时间为
t =
故滑块离开B后平抛时间与小车撤掉恒力F后运动时间相同。
由牛顿第二定律得:
μMg = Ma′
由运动学公式得
υ = a t − a′t′
由平抛规律得
h =
带入数据得:h = 0.8m
知识点
以初速为

正确答案
解析
由题意知: 





知识点
如图所示,装甲车在水平地面上以速度v0=20m/s沿直线前进,车上机枪的枪管水平,距地面高为h=1.8m。在车正前方竖直一块高为两米的长方形靶,其底边与地面接触。枪口与靶距离为L时,机枪手正对靶射出第一发子弹,子弹相对于枪口的初速度为v=800m/s。在子弹射出的同时,装甲车开始匀减速运动,行进s=90m后停下。装甲车停下后,机枪手以相同方式射出第二发子弹。(不计空气阻力,子弹看成质点,重力加速度g=10m/s2)
(1)求装甲车匀减速运动时的加速度大小;
(2)当L=410m时,求第一发子弹的弹孔离地的高度,并计算靶上两个弹孔之间的距离;
(3)若靶上只有一个弹孔,求L的范围。
正确答案
见解析
解析
解析:(1)由v20=2ax得
a=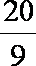
(2)由平抛公式
L=vt
y1=
解得y1≈1.31m
∴弹孔离地高度为H=1.8-y1=0.49m
同理发射第二发子弹时y2=0.8m
∴ d= y1-y2=0.51m
(3)因为水平距离不等,两发子弹不可能打到一个弹孔上。
即只有一发子弹打到靶上
由平抛公式
L=vt
y=
L=480m
当只有一发子弹打到靶上时,480m<L≤570m
知识点
扫码查看完整答案与解析

















