- 平行关系的综合应用
- 共147题
在△ABC中,内角A,B,C,的对边分别为a,b.c
(1)求角A的大小;
(2) 若a=
正确答案
见解析
解析
解:
(1) 由





(2) 由



得

知识点
已知函数f(x)=ax2-ln x,x∈(0,e],其中e是自然对数的底数,a∈R.
(1)当a=1时,求函数f(x)的单调区间与极值;
(2)是否存在实数a,使f(x)的最小值是3?若存在,求出a的值;若不存在,说明理由。
正确答案
见解析
解析
(1)∵f(x)=x2-ln x,f′(x)=2x-=,x∈(0,e],
令f′(x)>0,得<x<e,f′(x)<0,得0<x<,
∴f(x)的单调增区间是,单调减区间为.
∴f(x)的极小值为f=-ln=+ln 2.无极大值, …… 4分
(2)假设存在实数a,使f(x)=ax2-ln x,x∈(0,e]有最小值3,f′(x)=2ax-=。
①当a≤0时,x∈(0,e],所以f′(x)<0,所以f(x)在(0,e]上单调递减,
∴f(x)min=f(e)=ae2-1=3,a=(舍去)。
②当a>0时,令f′(x)=0,得x= ,(ⅰ)当0< <e,即a>时,
f(x)在上单调递减,在上单调递增
∴f(x)min=f=-ln=3,得a=。
(ⅱ)当≥e,即0<a≤时,x∈(0,e]时,f′(x)<0,所以f(x)在(0,e]上单调递减,∴f(x)min=f(e)=ae2-1=3,a=(舍去),此时f(x)无最小值。
综上,存在实数a=,使得当x∈(0,e]时,f(x)有最小值3. …… 14分
知识点
在如图所示的多面体






(1)求证:
(2)求多面体
正确答案
见解析。
解析
(1)
又因平面







(2)作



又



又



故多面体

知识点
7.若偶函数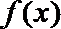
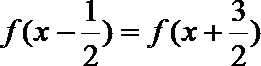
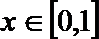
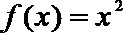
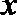
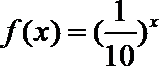
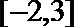
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析


















