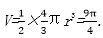- 平行关系的综合应用
- 共147题
13.在等腰梯形ABCD中,已知



正确答案
解析
在等腰梯形ABCD中,由




考查方向
解题思路
高考对平面向量数量积的考查主要是向量的模,夹角的运算及平行与垂直的判断与应用,在利用数量积的定义进行计算时,要善于将相关向量分解为图形中模与夹角已知的向量进行运算,运算时一定要注意向量的方向,搞清两向量的夹角.
易错点
向量的长度与夹角的计算
知识点
17.如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF||AB,AB=2,BC=EF=1,AE=
(Ⅰ)求证:FG||平面BED;
(Ⅱ)求证:平面BED⊥平面AED;
(Ⅲ)求直线EF与平面BED所成角的正弦值.
正确答案
知识点
14.如图,已知平面四边形ABCD,AB=BC=3,CD=1,AD=
正确答案
知识点
16.如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且

求证:(1)直线DE∥平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
正确答案
(1)


又





⑵ 


且



又

又

又







知识点
9.已知四棱锥P-ABCD的底面是正方形,侧棱PA⊥底面ABCD,底面对角线长AC=2,侧面PAB的面积为
正确答案
解析
设底面边长为a,依题意得a2=2, 

知识点
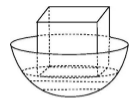
8.如图,有一个水平放置的半球形容器,内有高度为1的溶液,现将一个棱长为2的正方体放入其中,恰好能使液面和正方体的底面完全接触,则该半球形容器的容积为________
正确答案
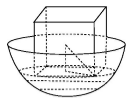
解析
作出如图所示辅助线,设半球的半径为r,则有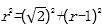
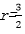
知识点
12.已知



正确答案
60°
解析
解析已在路上飞奔,马上就到!
知识点
12.空间直角坐标系O—xyz中,球心坐标为(-2,0,3),半径为4的球面方程是___________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如图所示,四边形







(Ⅰ)求证:
(Ⅱ)求

(III)求三棱锥
正确答案
见解析
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难.
(1)证明:取AB中点O,连结OD,OE








又



(2)





在
又

(3)解:
考查方向
解题思路
本题考查立体几何中的线面位置关系,解题步骤如下:1、利用线面垂直的性质定理。2、利用向量法转化。
易错点
1、第一问中的线线垂直的判定。2、第二问中求线面角时要利用向量法。
知识点
10.已知三棱锥





正确答案
解析
设底面




考查方向
解题思路
先由题中条件求出球的半径,再由球的表面积公式求表面积。
易错点
无法找到球与椎体的联系。
知识点
扫码查看完整答案与解析