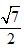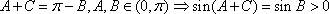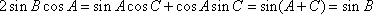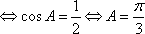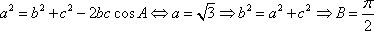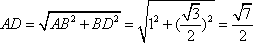- 平行关系的综合应用
- 共147题
请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
如图，长方体
（1）证明：
（2）如果
正确答案
见解析
解析
（I）连接
长方体
（2）在矩形
得：
知识点
设
A
B
C
D
正确答案
解析
化简
因为
知识点
函数f(x)＝xcos2x在区间[0,2π]上的零点的个数为( )
正确答案
解析
令f(x)＝xcos2x＝0，得x＝0或cos2x＝0，故x＝0或2x＝kπ＋
知识点
若函数
A
B
C3
D4
正确答案
解析
∵
当且仅当
知识点
如图，正方体ABCD-A1B1C1D1中，AB=2。，点E为AD的中点，点F在CD上，若EF∥平面AB1C，则线段EF的长度等于________。
正确答案
解析
由EF∥平面AB1C可得
EF=
知识点
已知向量
A
B
C6
D12
正确答案
解析
略
知识点
设△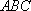
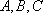
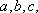
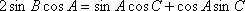
（1）求角A的大小；
（2）若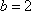
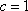
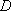
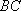
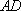
正确答案
（1）
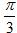
解析
（1）
（II）
在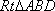
知识点
某几何体的三视图如图所示，则它的体积是（ ）
A
B
C8-2π
D
正确答案
解析
选A 由几何体的三视图可知几何体为一个组合体，
即一个正方体中间去掉一个圆锥体，所以它的体积是
知识点
如题（20）图，在四面体
（1）求四面体ABCD的体积；
（2）求二面角C-AB-D的平面角的正切值.
正确答案
（1） 
解析
（1）如答（20）图1，过D作DF⊥AC垂足为F，
故由平面ABC⊥平面ACD，知DF⊥平面ABC，即DF
是四面体ABCD的面ABC上的高，设G为边CD的中点，
则由AC=AD，知AG⊥CD，从而
由
故四面体ABCD的体积
（2）如答（20）图1，过F作FE⊥AB，垂足为E，连接DE.
由（1）知DF⊥平面ABC.
由三垂线定理知DE⊥AB，故∠DEF为二面角C—AB—D的平面角.
在
在
在Rt△DEF中，
知识点
扫码查看完整答案与解析