- 平行关系的综合应用
- 共147题
如图,在四棱锥P—ABCD中,底面ABCD为菱形,
(1)若PA=PD,求证:平面PQB
(2)点M往线段PC上,PM=tPC,试确定实数t的值,使PA//平面MQB。
正确答案
见解析
解析
(1)连结

且

又


又因为

又

又
……………………………6分
(2)证明:因为




由



因为





所以
因此,


知识点
在棱长为



①若

②若满足



正确答案
6;
解析
略
知识点
将1,2,3,…,9这9个正整数分别写在三张卡片上,要求每一张卡片上的任意两数之差都不在这张卡片上,现在第一张卡片上已经写有1和5,第二张卡片上写有2,第三张卡片上写有3,则6应该写在第()张卡片上;第三张卡片上的所有数组成的集合是()。
正确答案
二;
解析
略
知识点
若




正确答案
解析
略
知识点
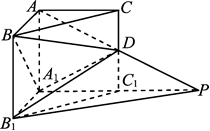
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=1,D是棱CC1上的一点,P是AD的延长线与A1C1的延长线的交点,且PB1∥平面BDA1。
(1)求证:CD=C1D;
(2)求二面角A-A1D-B的平面角的余弦值;
(3)求点C到平面B1DP的距离。
正确答案
见解析。
解析

∵BA⊥CA,BA⊥AA1,且AA1∩AC=A,∴BA⊥平面AA1C1C。
由三垂线定理可知BE⊥DA1,∴∠BEA为二面角A-A1D-B的平面角。
(3)由题意知,点C到平面B1DP的距离是点C到平面DB1A的距离, 设此距离为h.
∵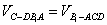
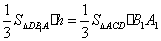
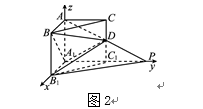
解法二:
如图2,以A1为原点,A1B1,A1C1,A1A所在直线分别为x轴,y轴,z轴建立空间直角坐标系A1-xyz,则A1(0,0,0),B1(1,0,0),C1(0,1,0),B(1,0,1)。
知识点
扫码查看完整答案与解析