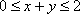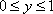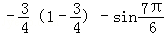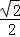- 平行关系的综合应用
- 共147题
1
题型:填空题
|
从字母

正确答案
解析
略
知识点
平行关系的综合应用
1
题型:填空题
|
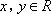
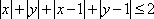
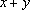
正确答案
解析
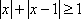
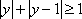

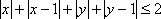
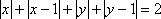
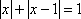
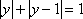

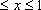

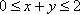
知识点
平行关系的综合应用
1
题型:填空题
|
若函数f(x)(x∈R)是周期为4的奇函数,且在[0,2]上的解析式为f(x)=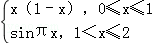
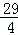
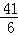
正确答案
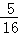
解析
函数f(x)(x∈R)是周期为4的奇函数,且在[0,2]上的解析式为f(x)=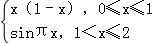
则f(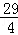
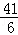
=f(8﹣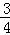
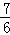
=f(﹣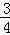
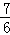
=﹣f(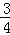
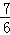
=
=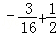
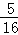
知识点
平行关系的综合应用
1
题型:简答题
|
设F1,F2分别是椭圆E: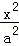
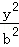
(1)若|AB|=4,△ABF2的周长为16,求|AF2|;
(2)若cos∠AF2B=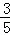
正确答案
(1)|AF2|=5
(2)e=
解析
(1)∵|AB|=4,|AF1|=3|F1B|,
∴|AF1|=3,|F1B|=1,
∵△ABF2的周长为16,
∴4a=16,
∴|AF1|+|AF2|=2a=8,
∴|AF2|=5;
(2)设|F1B|=k(k>0),则|AF1|=3k,|AB|=4k,
∴|AF2|=2a﹣3k,|BF2|=2a﹣k
∵cos∠AF2B=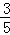
∴(4k)2=(2a﹣3k)2+(2a﹣k)2﹣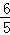
化简可得a=3k,
∴|AF2|=|AF1|=3k,|BF2|=5k
∴|BF2|2=|AF2|2+|AB|2,
∴AF1⊥AF2,
∴△AF1F2是等腰直角三角形,
∴c=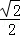
∴e=

知识点
平行关系的综合应用
1
题型:填空题
|
已知向量
正确答案
10
解析
知识点
平行关系的综合应用
已完结
扫码查看完整答案与解析