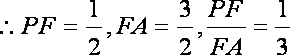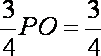- 平面与平面平行的判定与性质
- 共156题
在四棱锥








(1)求证: 平面

(2) 当


正确答案
见解析
解析
(1)证明: 过A作AF
所以
又



因为


所以
而


(2)连接BD交AC于点O, 连接EO, 因为



面
则


知识点
如图,在多面体






(1)在平面



(2)求直线

正确答案
见解析
解析
(1)存在点



证明:当点



∴

∴
又∵



∴

(2)连接


∵


∴

又∵

∴

∴ 


由已知可得,
∴

所以直线


知识点
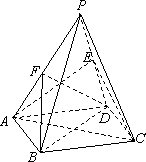
如图所示多面体中,AD⊥平面PDC,ABCD为平行四边形,E,F分别为AD,BP的中点,AD=


(1)求证:EF∥平面PDC;
(2)若∠CDP=90°,求证BE⊥DP;
(3)若∠CDP=120°,求该多面体的体积.
正确答案
见解析。
解析
(1)取PC的中点为O,连FO,DO,
∵F,O分别为BP,PC的中点,
∴

又ABCD为平行四边形,

∴
∴四边形EFOD是平行四边形 ---------------------------------------------2分
即EF∥DO 又EF
∴EF∥平面PDC。 --------------------------------------------- 4分
(2)若∠CDP=90°,则PD⊥DC,
又AD⊥平面PDC ∴AD⊥DP,
∴PD⊥平面ABCD, --------------------------------- 6分
∵BE
∴BE⊥DP -------------------------------- 8分
(3)连结AC,由ABCD为平行四边形可知

所以三棱锥

即五面体的体积为三棱锥
∵AD⊥平面PDC,∴AD⊥DP,由AD=3,AP=5,可得DP=4
又∠CDP=120°PC=2
由余弦定理并整理得
∴

∴该五面体的体积为
知识点
已知椭圆



(1)求椭圆的方程;
(2)设垂直于



(3) 过点




正确答案
见解析
解析
解:(1)由


(2)设

又

当且仅当
从而

(3)因为A(-1,0),所以
由


∴点
同理,有

∴

即
所以

知识点
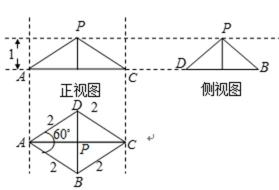
一个四棱锥的三视图和直观图如图所示,其中俯视图中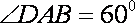
(1)求证:PB//平面AEC;
(2)若F为侧棱PA上的一点,且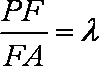
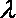

正确答案
见解析
解析
(1)由图形可知该四棱锥和底面ABCD是菱形,且有一角为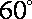
设AC,BD和交点为O,连OE,OE为△DPB的中位线,
OE//PB,EO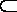
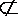
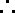
(2)过O作OF
在Rt△POA中,PO=1,AO=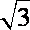
在棱形中BD


及BD

当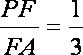

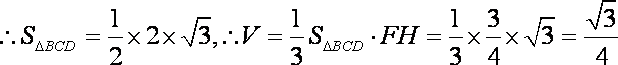
知识点
扫码查看完整答案与解析