- 平面与平面平行的判定与性质
- 共156题
设a,b,c为单位向量,a,b的夹角为600,则(a + b + c)·c的最大值为 。
正确答案
解析
略
知识点
已知




正确答案
2
解析
略
知识点
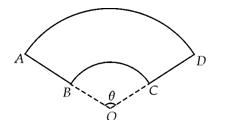
某公司承建扇环面形状的花坛如图所示,该扇环面花坛是由以点
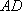
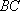
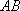
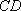
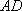
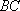

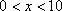
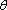
(1)求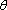

(2)在对花坛的边缘进行装饰时,已知两条线段的装饰费用为4元/米,两条弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为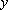

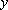
正确答案
(1)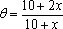
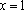
解析
(1)设扇环的圆心角为,则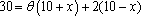
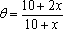
(2) 花坛的面积为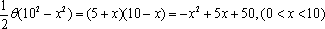
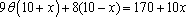
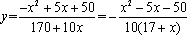
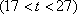
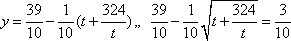
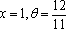
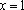
知识点
如图,四棱锥P—ABCD中,底面ABCD是菱形,PA= PD,
(1)求证:AD
(2)若Q是PC的中点,求证:PA∥平面BDQ;
(3)若

正确答案
见解析。
解析
(1)证明:
由E是AD的中点, PA=PD,所以AD⊥PE;
又底面ABCD是菱形,∠BAD=60
所以AB=BD,又因为E是AD的中点 ,
所以AD⊥BE,
又PE∩BE=E 所以AD⊥平面PBE.
(2)证明:连接AC交BD于点O,连OQ;因为O是AC的中点,
Q是PC的中点,所以OQ//PA,
又PA

(3)解:设四棱锥P-BCDE,Q-ABCD的高分别为
所以

又因为

所以
知识点
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,
(1)证明:A1BD // 平面CD1B1;
(2)求三棱柱ABD-A1B1D1的体积,
正确答案
见解析
解析
知识点
扫码查看完整答案与解析