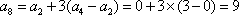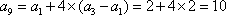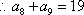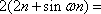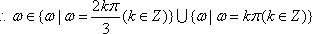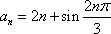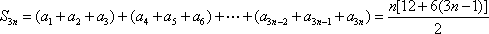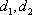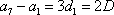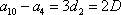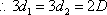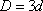- 平面与平面平行的判定与性质
- 共156题
如图1,在直角梯形



现以







(1)求证:

(2)求证:
(3)求点

正确答案
见解析。
解析
(1)证明:
取


在△


所以


由已知


所以


所以四边形
所以

又因为



所以

(2)在正方形

又因为平面



所以

所以
在直角梯形



在△

所以
所以
所以

(3)解法一:因为



过点




所以点


在直角三角形
所以
所以点


解法二:

所以
又


则 
所以点


知识点
已知直线m、n和平面α,在下列给定的四个结论中,m∥n的一个必要但不充分条件是
正确答案
解析
略
知识点
若数列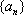

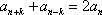
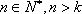
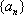
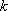
(1)已知数列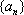
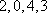
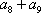
(2)若
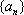
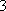
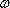
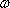
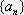

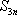
(3)若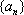
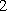
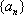
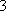
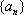
正确答案
见解析
解析
(1)
(2)


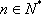
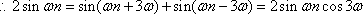
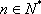
所以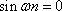
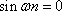
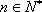
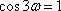
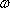
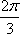
由于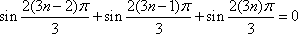
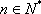

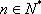
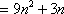
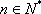
(3)若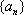
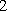
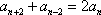
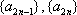
设等差数列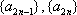
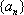
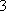
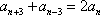

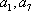
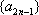
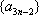
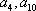

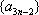
设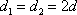
所以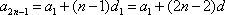
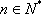
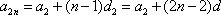
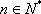
又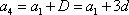

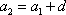
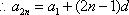
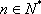
综合得: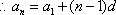
知识点
设a,b,c是空间三条直线,
正确答案
解析
略
知识点
已知
正确答案
解析
略
知识点
扫码查看完整答案与解析