- 平面与平面平行的判定与性质
- 共156题
1
题型:
单选题
|
三棱锥







正确答案
C
解析
在△

















知识点
平面与平面平行的判定与性质
1
题型:
单选题
|
在直三棱柱




正确答案
C
解析
如图,取



























知识点
平面与平面平行的判定与性质
1
题型:简答题
|
如图5,已知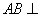
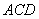
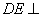
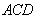
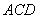
三角形,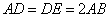
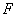
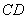
(1)求证: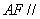
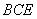
(2)求证:平面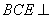
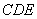
正确答案
见解析。
解析
证明:(1) 证:取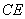
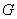
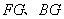
∵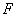
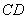
∴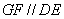

∵
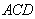
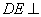
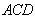
∴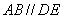
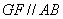
又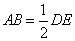
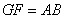
∴四边形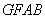
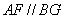
∵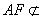
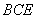
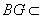
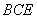
∴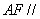
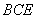
(2)求证:平面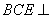
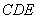
证:∵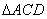
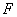
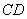
∴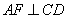
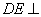
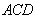
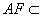
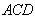
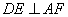
又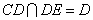
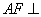
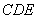
∵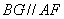
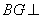
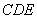
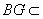
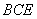
∴平面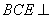
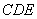
知识点
平面与平面平行的判定与性质
1
题型:
单选题
|
设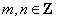
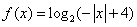
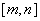

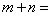
正确答案
C
解析
由题意,当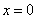
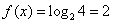
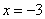
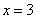
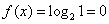

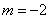
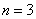
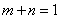
知识点
平面与平面平行的判定与性质
1
题型:
单选题
|
如图,正方体ABCD-A1B1C1D1的棱长为4,点P、Q在棱CC1上,PQ=1,


正确答案
A
解析
如图,连接


































知识点
平面与平面平行的判定与性质
下一知识点 : 平行关系的综合应用
扫码查看完整答案与解析