- 平面与平面平行的判定与性质
- 共156题
在如图所示的几何体中,四边形










(1)求证:

(2)求证:

正确答案
见解析。
解析
(1)连接






又因为 



所以 

(2)连结





所以 平面

因为 


所以 

因为 

所以 四边形

又 


则 



知识点
已知椭圆


(1)如图1,点






(2)如图2,直线






正确答案
见解析。
解析
(1)由已知得




整理得

由①②联立解得




(2)设











化简得
由



且
整理得




知识点
如图,在四棱锥



(1)若





(2)求证:
(3)若


正确答案
见解析
解析
(1)如图,连结
因为底面
所以

又因为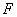

所以

在△




所以

又因为



所以

(2)因为平面



又


所以

又因为

所以

(3)在△

所以
由(2)可知

所以

又因为
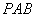
所以平面

知识点
已知 

① 



则上述结论中正确的个数为
正确答案
解析
略
知识点
三棱锥S-ABC的所有顶点都在球O的表面上,SA

正确答案
解析
略
知识点
扫码查看完整答案与解析





























