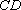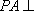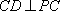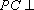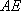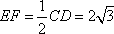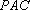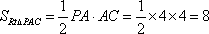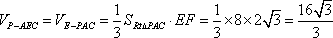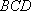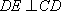- 平面与平面平行的判定与性质
- 共156题
下面四个命题:
①把函数


②函数



③正方体的内切球与其外接球的表面积之比为1∶3;
④“


其中所有正确命题的序号为 。
正确答案
②③
解析
略
知识点
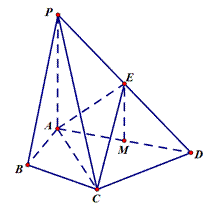
在四棱锥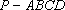
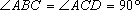
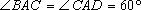
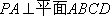
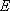
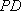
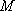
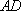
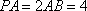
(1)求证: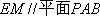
(2)求证: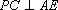
(3)求三棱锥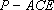
正确答案
见解析。
解析
解:
(1)因为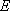
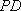
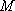
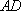
则在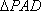
又
则 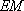
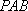
(2)证明 取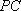
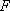
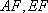
在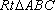
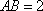
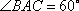
则 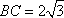
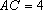
而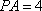
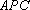
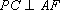
又 在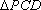
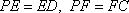
则 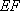
因为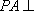
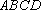
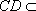
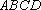
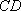
又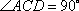
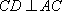
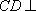
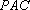
因此 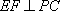
又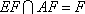
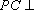
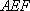
故
(3)由(1)(2)知 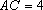
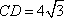
因为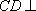
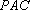
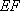
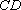
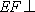
因此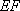
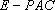
而
故
知识点
已知



正确答案
解析
略
知识点
已知某个几何体的三视图如图所示,则这个几何体的体积是 。
正确答案
6
解析
由已知中的三视图可得
该几何体是一个以俯视图为底面,
以2为高的四棱锥
故这个几何体的体积V=

故答案为:6
知识点
如图,几何体












(1)求证:
(2)求证:

正确答案
见解析。
解析
(1)连接




因为





所以四边形

因为




所以

(2)取


因为



因为




所以四边形
所以





所以

知识点
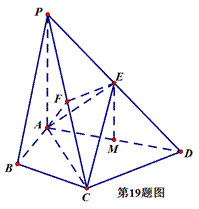
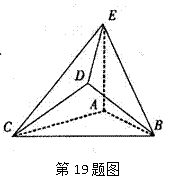
如图,AD

(1)求证:AF∥平面BDE;
(2)求证:平面BDE
正确答案
见解析。
解析
(1)证明:∵AD⊥平面ABC,AC

∴AD⊥AC,AD⊥AB,
∵AD∥CE,∴CE⊥AC
∴四边形ACED为直角梯形.……………(1分)
又∵∠BAC=90°,∴AB⊥AC,∴AB⊥面ACED.
………………(2分)
∴凸多面体ABCED的体积
求得CE=2.……………………………………………………(3分)
取BE的中点G,连结GF,GD,
则GF∥EC,GF
∴GF∥AD,GF=AD,四边形ADGF为平行四边形,
∴AF∥DG.………………………………………………………(5分)
又∵GD

∴AF∥平面BDE.………………………………………………(7分)
(2)证明:∵AB=AC,F为BC的中点,
∴AF⊥BC.………………………………………………………(8分)
由(1)知AD⊥平面ABC,AD∥GF,∴GF⊥面ABC.
∵AF
又BC
又∵DG∥AF,∴DG⊥面BCE.……………………………(11分)
∵DG
知识点
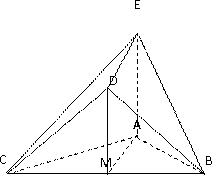
在如图所示的几何体中,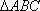
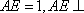
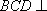
(1)AE//平面BCD;
(2)平面BDE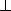
正确答案
见解析
解析
(1)
取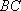
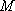
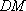
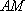
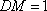
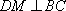
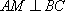
又因为平面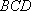
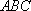
所以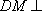
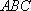
因为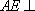
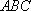
所以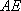
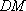
又因为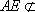
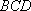
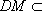
所以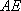
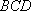
(2)由(1)知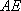
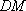
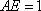
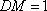
所以四边形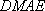
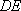
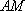
因为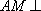
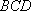
所以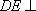
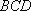
又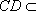
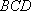
由已知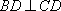
则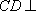
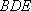
因为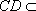
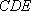
所以平面
(也可利用勾股定理证明题中的垂直关系.)
知识点
在如图所示的几何体中,四边形









(1)求证:

(2)在



正确答案
见解析
解析
(1)证明:取


在




所以
又因为
所以

所以四边形
所以
又因为



故

(2)解:假设在


因为


又因为


在

因为



显然,当

因为



易得

所以

知识点
已知直线l、m、n及平面

正确答案
解析
l和n可满足平行、相交、垂直等多种情况。
知识点
已知直线m,l,平面α,β,且m⊥α,l⊂β,给出下列命题:
①若α∥β,则m⊥l;②若α⊥β,则m∥l;
③若m⊥l,则α∥β④若m∥l,则α⊥β
其中正确命题的个数是( )
正确答案
解析
(1)中,若α∥β,且m⊥α⇒m⊥β,又l⊂β⇒m⊥l,所以①正确。
(2)中,若α⊥β,且m⊥α⇒m∥β,又l⊂β,则m与l可能平行,可能异面,所以②不正确。
(3)中,若m⊥l,且m⊥α,l⊂β⇒α与β可能平行,可能相交,所以③不正确。
(4)中,若m∥l,且m⊥α⇒l⊥α又l⊂β⇒α⊥β,∴④正确,故选B。
知识点
扫码查看完整答案与解析