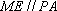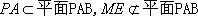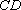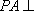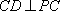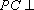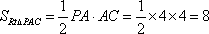- 平面与平面平行的判定与性质
- 共156题
1
题型:填空题
|
下面四个命题:
①把函数


②函数



③正方体的内切球与其外接球的表面积之比为1∶3;
④“


其中所有正确命题的序号为 。
正确答案
②③
解析
略
知识点
平面与平面平行的判定与性质
1
题型:简答题
|
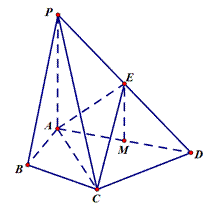
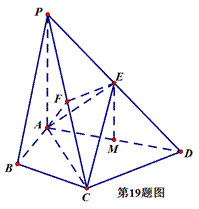
在四棱锥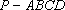
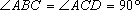
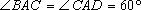
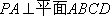
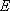
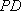
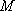
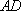
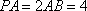
(1)求证: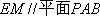
(2)求证: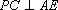
(3)求三棱锥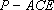
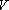
正确答案
见解析。
解析
解:
(1)因为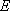
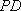
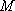
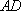
则在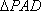
又
则 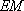
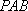
(2)证明 取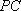
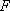
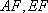
在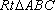
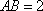
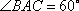
则 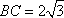
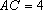
而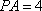
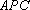
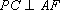
又 在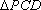
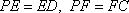
则 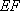
因为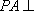
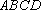
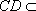
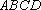
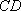
又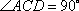
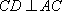
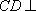
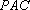
因此 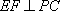
又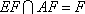
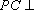
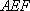
故
(3)由(1)(2)知 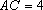
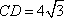
因为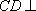
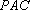
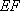
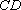
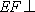
因此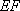
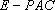
而
故
知识点
平面与平面平行的判定与性质
1
题型:
单选题
|
已知



正确答案
D
解析
略
知识点
平面与平面平行的判定与性质
1
题型:简答题
|
如图,几何体












(1)求证:
(2)求证:

正确答案
见解析。
解析
(1)连接




因为





所以四边形

因为




所以

(2)取


因为



因为




所以四边形
所以





所以

知识点
平面与平面平行的判定与性质
1
题型:
单选题
|
已知直线l、m、n及平面

正确答案
C
解析
l和n可满足平行、相交、垂直等多种情况。
知识点
命题的真假判断与应用直线与平面平行的判定与性质平面与平面平行的判定与性质直线与直线垂直的判定与性质直线与平面垂直的判定与性质
下一知识点 : 平行关系的综合应用
扫码查看完整答案与解析