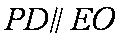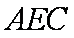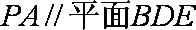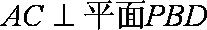- 平面与平面平行的判定与性质
- 共156题
如图,直三棱柱








(1)求异面直线

(2)求三棱锥
正确答案
见解析
解析
(1)过A作AQ∥C1N交A1C1于Q,连结



根据四边形
计算







由已知条件和余弦定理可得




(2)过








知识点
平面内一动点

(1)求
(2)求动点

(3)类似高二第二学期教材(12.4椭圆的性质、12.6双曲线的性质、12.8抛物线的性质)中研究曲线的方法请你研究轨迹C的性质,请直接写出答案(9分)
正确答案
见解析
解析
(1)
当且仅当


(2)

化简
(3)性质:对称性:关于原点对称
关于
关于
顶点:





知识点
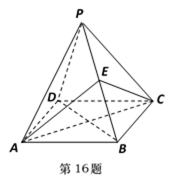
在四棱锥P-ABCD中,AB∥DC,AB⊥平面PAD, PD=AD,AB=2DC,E是PB的中点。
求证:(1)CE∥平面PAD;
(2)平面PBC⊥平面PAB。
正确答案
见解析。
解析
(1)
(方法1)取PA的中点F,连EF,DF。
因为E是PB的中点,所以EF // AB,且
因为AB∥CD,AB=2DC,所以EF∥CD,

从而CE∥DF,而

故CE∥平面PAD。
(方法2)取AB的中点M,连EM,CM,
因为E是PB的中点,所以EM // PA。
因为AB∥CD,AB=2DC,所以CM // AD。
因为

所以EM∥平面PAD,同理,CM∥平面PAD。
因为

所以平面CEM∥平面PAD,而
(2)(接(1)中方法1)因为PD=AD,且F是PA的中点,所以
因为AB⊥平面PAD,

因为CE∥DF,所以

因为


因为
知识点
已知函数

(1)当

(2)当



(3)当








正确答案
见解析
解析
(1)因为函数



所以

(2)




由题意可知:

所以

(3)由








由









所以


由①②可知,


知识点
如图,在直三棱柱


(1)求四棱锥
(2)求异面直线AE与A1C所成的角。
正确答案
见解析
解析
(1)四棱锥


∴
(2)取B1C1的中点E1,连A1E1,E1C,
则AE∥A1E1,∴∠E1A1C是异面直线AE与A1C所成的角。…(8分)
由






所以异面直线AE与A1C所成的角为
知识点
某粮仓是如图所示的多面体,多面体的棱称为粮仓的“梁”,现测得底面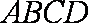
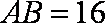
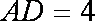
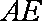
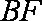
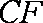
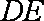
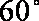
(1)求腰梁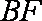
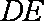
(2)若不计粮仓表面的厚度,该粮仓可储存多少立方米粮食?
正确答案
(1)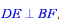
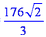
解析
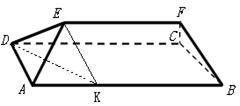
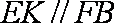

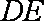
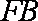
的角, (2分)

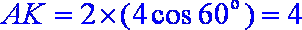
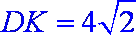


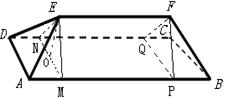


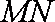
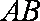
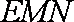

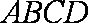
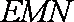
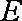


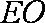
由题意知,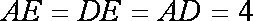
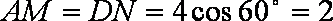
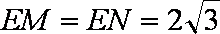

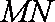
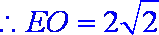
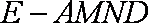
同理,再过点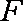

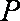
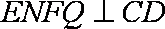
原多面体被分割为两个全等的四棱锥和一个直棱柱,且
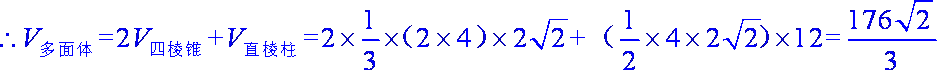
答:该粮仓可储存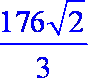
知识点
在棱长为4的正方体







正确答案
12
解析
考察在面CDD1C1上的投影,点A的投影为D,点G的投影为棱CC1的中点,当点E运动到A1时,其投影为D1,当点F运动到C1时投影仍为C1,此时该投影构成的图形面积最大。
知识点
如图,在四棱锥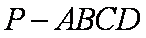
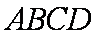
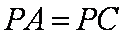
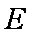
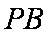
(1)求证: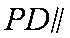
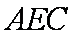
(2)求证:平面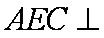
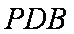
正确答案
见解析
解析
(1)证明:设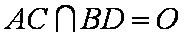
而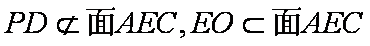
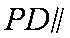
(2)连接PO,因为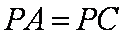

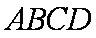
而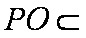
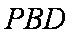
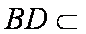
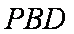
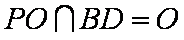

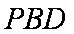
又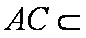
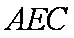
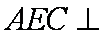
知识点
如图,在四棱锥








(1)求证:

(2)求证:
(3)设PD=AD=a, 求三棱锥B-EFC的体积.
正确答案
见解析。
解析
(1)证明:



(2)证明:









(3)
连接AC,DB相交于O,连接OF,
则OF⊥面ABCD,
∴
知识点
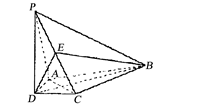
如图,在四棱锥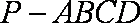
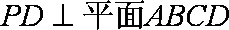

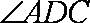
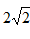
(1)证明PA//平面BDE;
(2)证明AC平面ACD;
(3)求直线BC与平面PBD所成的角的正切值。
正确答案
解析
(1)证明:设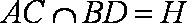
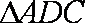
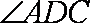
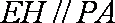
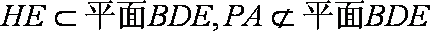
(2)证明:因为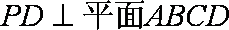
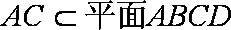
由(1)知,
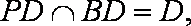
(3)解:由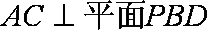
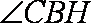
由
在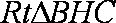
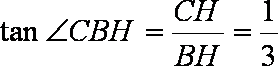

知识点
扫码查看完整答案与解析