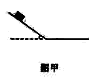- 匀变速直线运动的公式
- 共50题
如图所示,以A、B和C、D为端点的两半圆形光滑轨道固定于竖直平面内,一滑板静止在光滑水平地面上,左端紧靠B点,上表面所在平面与两半圆分别相切于B、C。一物块被轻放在水平匀速运动的传送带上E点,运动到A时刚好与传送带速度相同,然后经A沿半圆轨道滑下,再经B滑上滑板。滑板运动到C时被牢固粘连。物块可视为质点,质量为m,滑板质量M=2m,两半圆半径均为R,板长l =6.5R,板右端到C的距离L在R<L<5R范围内取值。E距A为s=5R。物块与传送带、物块与滑板间的动摩擦因素均为μ=0.5,重力加速度取g。
(1)求物块滑到B点的速度大小;
(2)试讨论物块从滑上滑板到离开滑板右端的过程中,克服摩擦力做的功Wf与L的关系,并判断物块能否滑到CD轨道的中点。
正确答案
见解析。
解析
(1)滑块从静止开始做匀加速直线运动到A过程,滑动摩擦力做正功,滑块从A到B,重力做正功,根据动能定理,

(2)滑块从B滑上滑板后开始作匀减速运动,此时滑板开始作匀加速直线运动,当滑块与滑板达共同速度时,二者开始作匀速直线运动。设它们的共同速度为v,根据动量守恒

对滑块,用动能定理列方程:
对滑板,用动能定理列方程:
由此可知滑块在滑板上滑过s1-s2=6R时,小于6.5R,并没有滑下去,二者就具有共同速度了。
当2R≤L<5R时,滑块的运动是匀减速运动8R,匀速运动L-2R,匀减速运动0.5R,滑上C点,根据动能定理:


当R<L<2R时,滑块的运动是匀减速运动6.5R+L,滑上C点。根据动能定理:

当
知识点
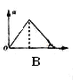
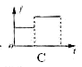
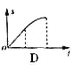
如图所示,物体沿斜面由静止滑下,在水平面上滑行一段距离停止,物体与斜面和水平面间的动摩擦因数相同,斜面与水平面平滑连接。图乙中
正确答案
解析
对物体进行受力分析和过程分析知,在斜面和水平面受到的合力均为恒力,两段均为匀变速运动,所以A、B都不对;第一段摩擦力小于第二段,所以C正确;路程随着时间的变化,开始也是非线性变化,所以D错误。
知识点
一个质量为0.1kg的小球从空中静止下落,与水平地面相碰后弹到空中某一高度,其速度随时间变化的关系如下图所示,则
正确答案
解析
略
知识点
24.如图所示,绷紧的传送带与水平面的夹角θ=30°,皮带在电动机的带动下,始终保持v0=2m/s的速率运行。现把一质量m=10kg的工件(可看做质点)轻轻放在皮带的底端,经时间t=1.9s,工件被传送到h=1.5m的高处,取g=10m/s2。求:
(1)工件与皮带间的动摩擦因数;
(2)电动机由于传送工件多消耗的电能。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
24.百米赛跑中,运动员的运动可以简化为如下过程:第一阶段从静止开始做匀加速直线运动,达到最大速度后做匀速直线运动到达终点。某运动员赛跑过程中能达到的最大速度为12m/s,该运动员至少以多大加速度起跑才能保证赛跑成绩在10s以内?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析