对数与对数函数_章节学习

1

题型：单选题

|

单选题 · 5 分

9.函数在的图像大致为

A

B

C

D

正确答案

D

解析

考查方向

函数图像与性质

解题思路

利用间接法,即由函数性质排除不符合条件的选项.

易错点

利用排除法合理的选择

知识点

对数函数的定义

1

题型：单选题

|

单选题 · 5 分

10．设直线l1，l2分别是函数f(x)= 图象上点P1，P2处的切线，l1与l2垂直相交于点P，且l1，l2分别与y轴相交于点A，B则则△PAB的面积的取值范围是（）

A(0,1)

B(0,2)

C(0,+∞)

D(1,+ ∞)

正确答案

A

解析

设（不妨设），则由导数的几何意义易得切线的斜率分别为由已知得切线的方程分别为，切线的方程为，即。分别令得又与的交点为，故选A。

考查方向

本题考查了1.导数的几何意义；2.两直线垂直关系；3.直线方程的应用；4.三角形面积取值范围，是高考当中重要的内容。

解题思路

本题首先考查导数的几何意义，其次考查最值问题，解题时可设出切点坐标，利用切线垂直求出这两点的关系，同时得出切线方程，从而得点坐标，由两直线相交得出点坐标，从而求得面积，题中把面积用表示后，可得它的取值范围．解决本题可以是根据题意按部就班一步一步解得结论．这也是我们解决问题的一种基本方法，朴实而基础，简单而实用．

易错点

本题考查导数的几何意义，其次考查最值问题，解题时可设出切点坐标，在求切线方程的时候易错。

知识点

对数函数的定义

1

题型：简答题

|

简答题 · 14 分

本题共有2个小题，第1小题满分6分，第2小题满分8分.

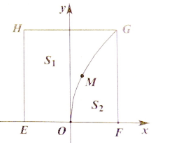
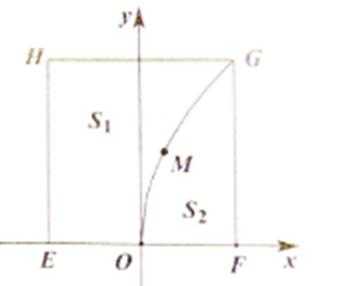
有一块正方形菜地EFGH，EH所在直线是一条小河，收获的蔬菜可送到F点或河边运走.于是，菜地分为两个区域S1和S2，其中S1中的蔬菜运到河边较近，S2中的蔬菜运到F点较近，而菜地内S1和S2的分界线C上的点到河边与到F点的距离相等.现建立平面直角坐标系，其中原点O为EF的中点，点F的坐标为（1，0），如图

21.求菜地内的分界线C的方程；

22.菜农从蔬菜运量估计出S1面积是S2面积的两倍，由此得到S1面积的“经验值”为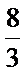 .设M是C上纵坐标为1的点，请计算以EH为一边、另有一边过点M的矩形的面积，及五边形EOMGH的面积，并判别哪一个更接近于S1面积的“经验值”.

第(1)小题正确答案及相关解析

正确答案

（）

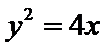
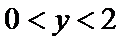
解析

因为上的点到直线与到点的距离相等，所以是以为焦点、以

为准线的抛物线在正方形内的部分，其方程为（）．

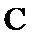
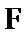
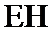
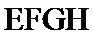
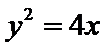
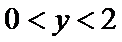
考查方向

抛物线的定义

解题思路

根据抛物线定义得到C的方程

易错点

题意的理解

第(2)小题正确答案及相关解析

正确答案

五边形面积更接近于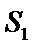面积的“经验值”．

解析

解：

依题意，点的坐标为．

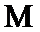
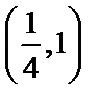
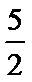
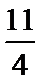
所求的矩形面积为，而所求的五边形面积为．

矩形面积与“经验值”之差的绝对值为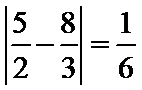，而五边形面积与“经验值”之差

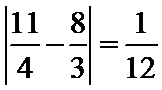
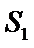
的绝对值为，所以五边形面积更接近于面积的“经验值”．

考查方向

理解、运算能力

解题思路

求出面积，根据题意比较和经验值的差距.

易错点

题意的理解

1

题型：填空题

|

填空题 · 5 分

16.设是奇函数的导函数，当时，，则使得成立的x的取值范围是 .

正确答案

解析

令,所以，所以g(x)在上为增函数，同理可知，g(x)在为增函数，因为g(x)为偶函数。所以可得当f(x)>0，时，x成立的取值范围为

考查方向

函数的性质及应用；导数的综合应用

解题思路

先根据导函数的正负判断函数的增减性，然后结合不等式得到答案。

易错点

对导数的性质掌握不好

知识点

对数函数的定义

1

题型：单选题

|

单选题 · 5 分

11．函数的定义域和值域都是[0，1]，则等于（）

A

B

C

D2

正确答案

D

解析

解析已在路上飞奔，马上就到！

知识点

对数函数的定义域对数函数的值域与最值

1

题型：单选题

|

单选题 · 5 分

设，函数的定义域为，值域为.定义“区间的长度等于”.若区间的长度的最小值为，则实数的值为

A11

B6

C

D6或

正确答案

B

解析

略

知识点

对数函数的值域与最值

1

题型：单选题

|

单选题 · 5 分

函数的值域为

AR

B

C

D

正确答案

C

解析

略

知识点

对数函数的值域与最值

1

题型：单选题

|

单选题 · 5 分

函数的值域为

A

B

C

D

正确答案

A

解析

因为，所以，故选A。

知识点

函数的值域及其求法对数函数的值域与最值

1

题型：简答题

|

简答题 · 14 分

18.设函数，且.

（1）求的值及的定义域；

（2）求在区间上的值域。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

对数的运算性质对数函数的定义域对数函数的值域与最值

1

题型：简答题

|

简答题 · 12 分

17．设函数f(x)＝log2(ax－bx) 且f(1)＝1，f(2)＝log212．

（1）求a、b的值；

（2）当x∈[1,2]时，求f(x)的最大值．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

对数的运算性质对数函数的值域与最值

热门试卷

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点