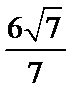- 与圆有关的比例线段
- 共49题
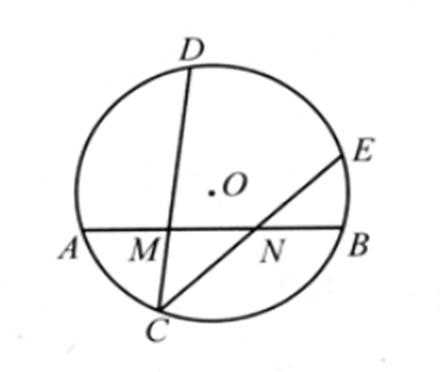
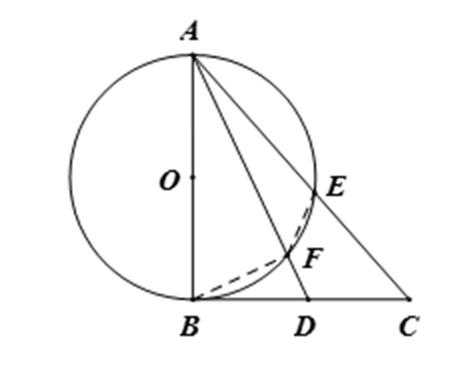
6.如图,在圆O中,M,N是弦AB的三等分点,弦CD,CE分别经过点M,N,若CM=2,MD=4,CN=3,则线段NE的长为( )
正确答案
解析
根据相交弦定理可得 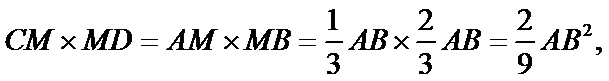
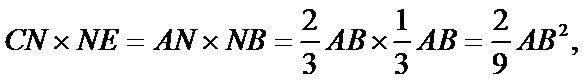
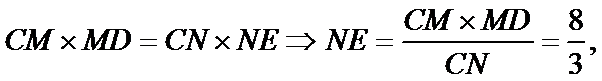
考查方向
解题思路
平面几何中与圆有关的性质与定理是高考考查的热点,解题时要充分利用性质与定理求解,本部分内容中常见的命题点有:平行线分线段成比例定理;三角形的相似与性质;圆内接四边形的性质与判定;相交弦定理与切割线定理.
易错点
相交弦定理的灵活运用
知识点
22.如图所示,











(1)求证
(2)求
正确答案
(1)见解析;(2)
解析
试题分析:本题属于割线定理及角平分线的性质的问题,1)直接利用三角形相似对应边成比例在化为乘积式即可得到相应的证明;(2)利用角平分线的性质转化为已知线段的比值。
(1)证明:由已知可得



(2)由切割线定理可得PB=1,





考查方向
解题思路
本题考查割线定理及角平分线的性质的问题,解题步骤如下:(1)直接利用三角形相似对应边成比例在化为乘积式即可得到相应的证明;(2)利用角平分线的性质转化为已知线段的比值。
易错点
第2问不会转化要求的比值。
知识点
22.已知四边形ABCD内接于⊙O,AD:BC=1:2,BA、CD的延长线交于点E,且EF切⊙O于F.
(Ⅰ)求证:EB=2ED;
(Ⅱ)若AB=2,CD=5,求EF的长.
正确答案
(1)见解析;(2)EF=2
解析
试题分析:本题属于几何证明选讲中有关线段成比例的定理,
(1)利用三角形相似对应边成比例即可得证;
(2)切割线定理的使用。
考查方向
解题思路
本题考查几何证明选讲中有关线段成比例的定理,解题步骤如下:
(1)利用三角形相似对应边成比例即可得证;
(2)切割线定理的使用。
易错点
定理不熟。
知识点
22.如图,在直角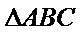

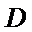

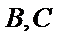
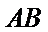

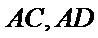
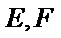
(Ⅰ)证明: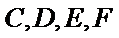
(Ⅱ)若
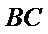
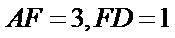
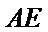
正确答案
(Ⅰ)略
(Ⅱ)
解析
试题分析:本题是有关直线与圆的问题,难度不大。在解题中注意结合切线的性质和勾股定理等知识进行解决。
(Ⅰ)连结
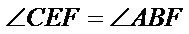
因为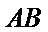
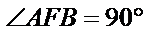
因为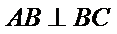

所以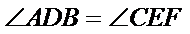
所以
(Ⅱ)由已知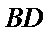

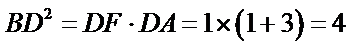
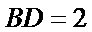
所以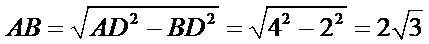
因为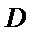
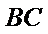
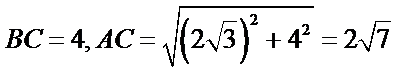
因为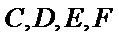
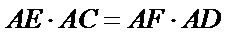
所以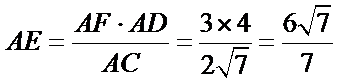
考查方向
解题思路
本题主要考查圆的基本性质、圆周角定理等基础知识。
解题步骤如下:利用四点共圆的判定定理,证明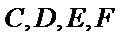
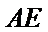
易错点
第二问计算中,不易想到利用第一问
知识点
22.选修4-1:几何证明选讲
如图,已知:














(Ⅰ)求证:∠BCF=∠CAB ;
(Ⅱ)若FB=FE=1,求⊙O的半径.
正确答案
(1)略
(2)
解析
(Ⅰ)证明:因为AB是直径,
所以∠ACB=90°
又因为F是BD中点,所以∠BCF=∠CBF=90°-∠CBA=∠CAB
因此∠BCF=∠CAB
(Ⅱ)解:直线CF交直线AB于点G,
由FC=FB=FE得:∠FCE=∠FEC
可证得:

且AB=BG
由切割线定理得:(1+FG)2=BG×AG=2BG2 ……①
在Rt△BGF中,由勾股定理得:BG2=FG2-BF2 ……②
由①、②得:FG2-2FG-3=0
解之得:FG1=3,FG2=-1(舍去)
所以AB=BG=
所以⊙O半径为
考查方向
解题思路
第一问:由已知条件得FC=FB=FE得到∠BCF=∠CBF=∠CAB
第二问:由FC=FB=FE得:∠FCE=∠FEC,继而证得:

易错点
1、第一问想到弦切角定理,进而向证明CF与圆相切,虽然可以证明,但是,但是过程稍烦一些。 2、第二问没有注意题中的已知条件,而运用
知识点
11. 如下图,





则
正确答案
解析


所以
设

求得,
由勾股定理可得,

所以
所以
考查方向
解题思路
根据切线长定理,勾股定理求解
易错点
圆中线段关系弄错
知识点
正确答案
知识点
22. 如图,














(Ⅰ)

23. 在直角坐标系中,曲线








(Ⅰ)求点






24. 已知函数
(Ⅰ)若



正确答案
22.略
23. (Ⅰ)
24. (Ⅰ)

解析
22. (Ⅰ)证明:连接


因为:

由弦切角等于同弦所对的圆周角:
所以:



(Ⅱ)由切割线定理得:
因为
所以:
由相交弦定理得:
所以:
23. (Ⅰ)由极值互化公式知:点




消去参数


(Ⅱ)点

将直线的参数方程代入曲线

设其两个根为

所以:

由参数

24. (Ⅰ)当
解得:
所以原不等式解集为
(Ⅱ)

只需:
解得:

考查方向
22.几何证明的相关知识
23. 参数方程和极坐标第
24. 本题考查了绝对值不等式的运用
解题思路
22.运用同圆中同弧或等弧所对的角相等,第二题中运用相交弦定理和切割线定理解决,注意进行线段关系的转化。
23. 按步骤解题
24.无
易错点
22.1.解题不规范 2.出边和角的关系。
23. 基础知识不扎实倒致错误。
24. 绝对值不等式不会运用
知识点
22.几何证明选讲
如图,











(1) 求证:
(2) 求证:
正确答案
答案已在路上飞奔,马上就到!
解析
(1)由







(2)由






考查方向
本题综合考查了圆的性质、弦切角定理、等边三角形的性质、三角形全等、三角形的外接圆的半径等知识,需要较强的推理能力、分析问题和解决问题的能力了与圆有关的比例线段
解题思路
(1)利用圆的切线的性质,结合等腰三角形的性质,即可证明∠PAD=∠CDE;
(2)利用△PBD∽△PEC,结合切割线定理即可证明结论.
易错点
圆的切线的性质不会灵活应用
知识点
22.选修4-1:几何证明选讲
如图,












(Ⅰ)求证:

(Ⅱ)若

正确答案
见解析
解析
试题分析:本题属于平面几何中的基本问题,题目的难度是容易题。
(Ⅰ)连接

又




(Ⅱ)过




设

由


可得
考查方向
本题考查了平面几何的知识,主要涉及直线与圆的位置关系,三角形相似的考查.
解题思路
本题考查平面几何的知识,解题步骤如下:
(1)利用圆的相关定理证明。
(2)利用切割线定理和相交弦定理证明。
易错点
相关的定理容易混用。
知识点
扫码查看完整答案与解析