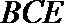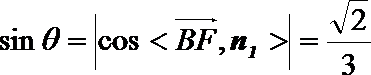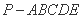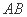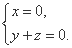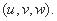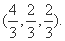- 空间向量及其应用、空间角
- 共58题
13.已知向量


正确答案
知识点
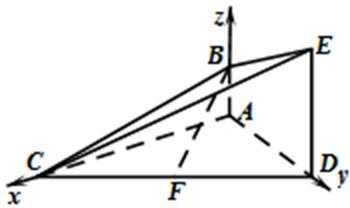
19.已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等腰直角三角形,AC⊥AD,且AD=DE=2AB,F为CD中点。
(Ⅰ)求证:平面BCE⊥平面CDE;
(Ⅱ)求直线BF和平面BCE所成角的正弦值。
正确答案
以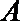
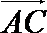
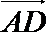
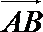
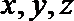
设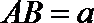
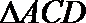
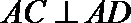
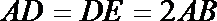
所以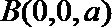
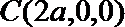
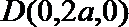
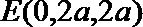
所以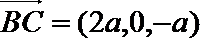
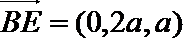
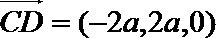
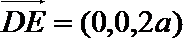
(Ⅰ)设平面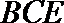
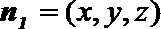
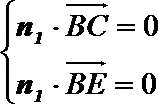
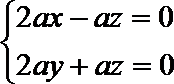
令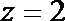
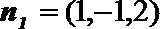
设平面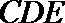
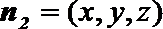
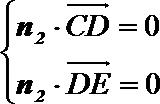
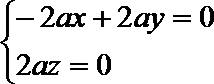
令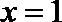
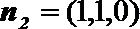
所以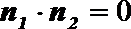
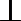
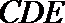
(Ⅱ)因为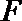
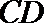
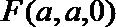
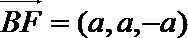
则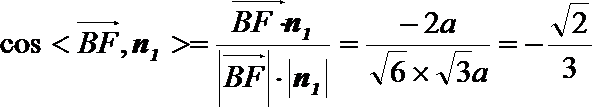
设直线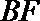
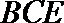
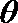
所以直线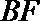
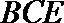
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,在三棱锥




(Ⅰ)若



(Ⅱ)若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.直三棱柱


△



正确答案
解析
由题意设底面正△ABC的边长为a,过P作PO⊥平面ABC,垂足为O,则点O为底面△ABC的中心,故∠PAO即为PA与平面ABC所成角。
又直三棱柱的体积为
所以只棱柱体积为
所以PA与平面ABC所称的角为
考查方向
直线与平面所成的角;棱柱、棱锥、棱台的体积
解题思路
由题意设底面正△ABC的边长为a,过P作PO⊥平面ABC,垂足为O,则点O为底面△ABC的中心,故∠PAO即为PA与平面ABC所成角,由此能求出PA与平面ABC所成的角.
易错点
空间感不强,计算化简能力弱
知识点
收到建设工程竣工报告后,( )应当组织设计、施工、工程监理等有关单位进行工程竣工验收。
A.物业服务企业
B.建设单位
C.施工单位
D.政府主管部门
正确答案
B
解析
暂无解析
如图,四棱锥P-ABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD=
(1)求PA的长;
(2)求二面角B-AF-D的正弦值。
正确答案
(1) 
解析
(1)
如图,连接BD交AC于O,因为BC=CD,即△BCD为等腰三角形,又AC平分∠BCD,故AC⊥BD。以O为坐标原点,







因PA⊥底面ABCD,可设P(0,-3,z),由F为PC边中点,F
又



因AF⊥PB,故

即6-


所以|

(2)由(1)知





由n1·

因此可取n1=(3,
由n2·

得

从而法向量n1,n2的夹角的余弦值为
cos〈n1,n2〉=
故二面角B-AF-D的正弦值为
知识点
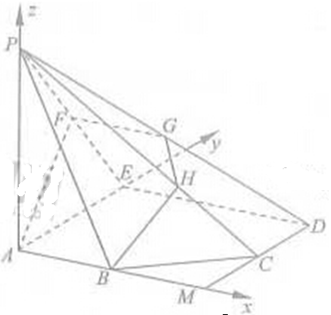
如图,正方形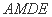
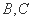
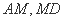
中,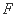
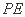
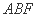
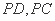

(1)求证: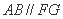
(2)若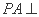
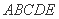
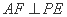
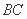
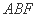
求线段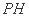
正确答案
见解析。
解析
(1)在正方形中,因为B是AM的中点,所以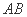
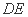
又因为
所以
因为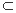
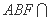
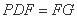
所以
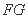
(2)因为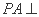
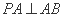
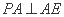
如图建立空间直角坐标系
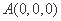
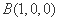
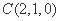

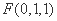
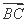
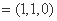
设平面ABF的法向量为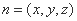
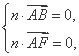
令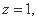
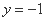
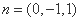
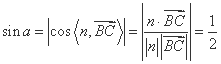
因此直线BC与平面ABF所成角的大小为
设点H的坐标为
因为点H在棱PC上,所以可设
即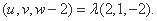
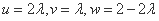
因为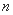
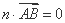
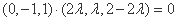
解得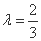
所以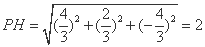
知识点
如图,在四棱锥P—ABCD中,底面是边长为

(1)证明:MN∥平面ABCD;
(2) 过点A作AQ⊥PC,垂足为点Q,求二面角A—MN—Q的平面角的余弦值。
正确答案
见解析
解析
本题主要考察线面平行的证明方法,建系求二面角等知识点。
(1)如图连接BD.
∵M,N分别为PB,PD的中点,
∴在
又MN
∴MN∥平面ABCD;
(2)如图建系:
A(0,0,0),P(0,0,


N(

设Q(x,y,z),则
∵

由


对于平面AMN:设其法向量为
∵
则

同理对于平面AMN得其法向量为
记所求二面角A—MN—Q的平面角大小为
则
∴所求二面角A—MN—Q的平面角的余弦值为
知识点
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱AB上的动点。
(1)求证:DA1⊥ED1 ;
(2)若直线DA1与平面CED1成角为45o,求
正确答案
见解析
解析
以D为坐标原点,建立如图所示的坐标系,则D(0,0,0),A(1,0,0),
B(1,1,0),C(0,1,0),D1(0,1,2),A1(1,0,1),设E(1,m,0)(0≤m≤1)
(1)证明:
所以DA1⊥ED1. ----------4分
(2)设平面CED1的一个法向量为


所以

因为直线DA1与平面CED1成角为45o,所以
所以


知识点
扫码查看完整答案与解析