- 简单组合体的结构特征
- 共10题
已知正四棱锥O－ABCD的体积为
正确答案
24π
解析
如图所示，在正四棱锥O－ABCD中，VO－ABCD＝
∴|OO1|＝
在Rt△OO1A中，OA＝
∴S球＝4πR2＝24π
知识点
已知某几何体的三视图(单位：cm)如图所示，则该几何体的体积是( )。
正确答案
解析
由三视图可知，该几何体是如图所示长方体去掉一个三棱锥，故几何体的体积是6×3×6－
知识点
如图，网格纸上正方形小格的边长为1（表示1cm），图中粗线画出的是某零件的三视图，该零件由一个底面半径为3cm，高为6cm的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为（ ）
A
B
C
D
正确答案
解析
几何体是由两个圆柱组成，一个是底面半径为3高为2，一个是底面半径为2，高为4，
组合体体积是：32π•2+22π•4=34π，底面半径为3cm，高为6cm的圆柱体毛坯的体积为：32π×6=54π。
切削掉部分的体积与原来毛坯体积的比值为：
知识点
若某几何体的三视图（单位：cm）如图所示，则此几何体的体积是
A
B
C
D
正确答案
解析
选B，本题主要考察了对三视图所表达示的空间几何体的识别以及几何体体积的计算，属容易题
知识点
圆柱M的底面直径与高均等于球O的直径，则圆柱M与球O的体积之比
正确答案
3：2
解析
略
知识点
如图，在正四棱柱
（1）当
（2）当
正确答案
（1）
解析
建立如图所示的空间直角坐标系
设
则各点的坐标为
所以
设平面DMN的法向量为
即
则
（1）因为
解得
所以
（2）因为
所以
因为
解得
根据图形和（1）的结论可知
知识点
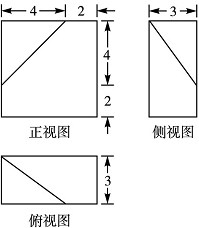
某几何体的三视图（单位：cm）如图所示，则该几何体的的体积是（ ）
正确答案
解析
由三视图知，原几何体是由一个长方体与一个三棱柱组成，其体积为
知识点
某几何体的正视图和侧视图均如图1所示，则该几何体的俯视图不可能是
A
B
C
D
正确答案
解析
本题是组合体的三视图问题，由几何体的正视图和侧视图均如图1所示知，原图下面图为圆柱或直四棱柱，上面是圆柱或直四棱柱或下底是直角的三棱柱，Ａ，Ｂ，Ｃ，都可能是该几何体的俯视图，Ｄ不可能是该几何体的俯视图，因为它的正视图上面应为如图的矩形.
知识点
某空间组合体的三视图如图所示，则该组合体的体积为（ ）
正确答案
解析
略
知识点
某几何体的三视图如图所示，则这个几何体的体积为
A4
B
C
D8
正确答案
解析
由三视图可知，该几何体可分为一个三棱锥和一个四棱锥，则
知识点
扫码查看完整答案与解析