- 全(特)称命题的否定
- 共44题
4.命题“

正确答案
解析






考查方向
解题思路
全称量词否定是特称量词,特称量词否定是全称量词
易错点
全称量词与特称量词复合命题的否定形式的不确定。
知识点
12.若“



正确答案
1
解析
“



实数m的最小值为:1.故答案为:1.
考查方向
解题思路
求出正切函数的最大值,即可得到m的范围.
易错点
命题的真假判断与应用.菁优网版权所有
知识点
13.命题“
正确答案
解析
利用命题的否定形式可得:
考查方向
解题思路
抓住两点一个是量词的否定,一个是结论的否定既可以直接得到答案。
易错点
就是不等号问题,属于典型错误。
知识点
4.命题“
正确答案
解析
试题分析:由全称命题的否定是特称命题,得出结论即可。
“


故选D.
考查方向
解题思路
根据全称命题的否定,把任意改为存在,然后否定结论即可.
易错点
注意含有量词的命题的否定中把任意改为存在,且的否定为或.
知识点
设函数

26.讨论函数
27.若


正确答案
当

当

当

解析
(Ⅰ)由题意知 函数


令
(1)当

此时


(2)当

①当





②当

设方程

因为
所以
由 

所以 当


当


当


因此 函数有两个极值点。
(3)当

由

当


当


所以函数有一个极值点。
综上所述:
当

当

当

考查方向
解题思路
(I)函数f(x)=ln(x+1)+a(x2﹣x),其中a∈R,x∈(﹣1,+∞).
(2)当a>0时,△=a(9a﹣8).①当

(3)当a<0时,△>0.即可得出函数的单调性与极值的情况.
易错点
分类讨论函数取得极值的情况,注意函数单调性的制约作用。
正确答案
(Ⅱ)
解析
(II)由(I)知,
(1)当


因为 
所以 

(2)当


所以 函数

又


(3)当


所以

因为
所以

(4)当

因为
所以 

因此 当

即
可得 
当

此时 
综上所述,
考查方向
解题思路
(II)由(I)可知:(1)当
(2)当
(3)当1<a时,由g(0)<0,可得x2>0,利用x∈(0,x2)时函数f(x)单调性,即可判断出;
(4)当a<0时,设h(x)=x﹣ln(x+1),x∈(0,+∞),研究其单调性,即可判断出
易错点
利用导数研究函数恒成立问题,注意转化与化归思想的应用.菁优网版权所有
3
①“p∨q”为真是“¬p”为假的必要不充分条件;
②“




其中说法正确的是( )
正确答案
解析
对于命题1,由¬p为假可以推出p∨q为真,但由p∨q为真不能推出¬p为假的值,所以前者是后者的必要不充分条件,命题1正确。易得命题2也是正确的。所以选C
考查方向
解题思路
根据相关性质,逐一判断
易错点
对逻辑与命题理解不透彻;
知识点
2.命题“存在

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知命题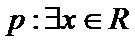
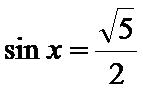
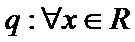
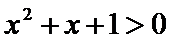
① 题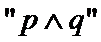
②命题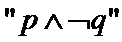
③命题
④命题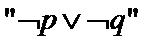
其中正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.命题“对任意的

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.命题“
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析




































