圆的参数方程
共13题

· 圆的参数方程

圆的参数方程
共13题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

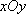
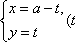
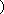
（坐标系与参数方程选做题）在平面直角坐标系中，直线为参数与

圆为参数相切，切点在第一象限，则实数的值为 .

正确答案

解析

略

知识点

参数方程化成普通方程直线的参数方程圆的参数方程

题型：简答题

简答题 · 10 分

已知动点P，Q都在曲线C：(t为参数)上，对应参数分别为t＝α与t＝2α(0＜α＜2π)，M为PQ的中点。

(1)求M的轨迹的参数方程；

(2)将M到坐标原点的距离d表示为α的函数，并判断M的轨迹是否过坐标原点。

正确答案

(1) (α为参数，0＜α＜2π)； (2)略

解析

(1)依题意有P(2cos α，2sin α)，Q(2cos 2α，2sin 2α)，

因此M(cos α＋cos 2α，sin α＋sin 2α)。

M的轨迹的参数方程为(α为参数，0＜α＜2π)。

(2)M点到坐标原点的距离

d＝(0＜α＜2π)。

当α＝π时，d＝0，故M的轨迹过坐标原点。

知识点

相关点法求轨迹方程圆的参数方程

题型：填空题

填空题 · 5 分

在平面直角坐标系xoy中，直线l的参数方程是（参数tR），圆C的参数方程是（参数θR），则圆C的圆心到直线l的距离为____________。

正确答案

解析

略

知识点

点到直线的距离公式参数方程化成普通方程直线的参数方程圆的参数方程

题型：简答题

简答题 · 10 分

已知曲线C1的参数方程为(t为参数)，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ＝2sin θ.

（1）把C1的参数方程化为极坐标方程；

（2）求C1与C2交点的极坐标(ρ≥0,0≤θ＜2π)。

正确答案

（1）ρ2－8ρcos θ－10ρsin θ＋16＝0.

（2），

解析

（1）将消去参数t，化为普通方程(x－4)2＋(y－5)2＝25，

即C1：x2＋y2－8x－10y＋16＝0.

将代入x2＋y2－8x－10y＋16＝0得ρ2－8ρcos θ－10ρsin θ＋16＝0.

所以C1的极坐标方程为

ρ2－8ρcos θ－10ρsin θ＋16＝0.

（2）C2的普通方程为x2＋y2－2y＝0.

由

解得或

所以C1与C2交点的极坐标分别为，.

知识点

简单曲线的极坐标方程极坐标刻画点的位置极坐标系和平面直角坐标的区别圆的参数方程

题型：简答题

简答题 · 10 分

已知动点P，Q都在曲线C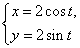：(t为参数)上，对应参数分别为t＝α与t＝2α(0＜α＜2π)，M为PQ的中点。

（1）求M的轨迹的参数方程；

（2）将M到坐标原点的距离d表示为α的函数，并判断M的轨迹是否过坐标原点。

正确答案

见解析

解析

（1）依题意有P(2cos α，2sin α)，Q(2cos 2α，2sin 2α)，

因此M(cos α＋cos 2α，sin α＋sin 2α)。

M的轨迹的参数方程为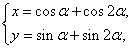(α为参数，0＜α＜2π)。

（2）M点到坐标原点的距离

d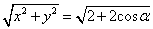＝(0＜α＜2π)。

当α＝π时，d＝0，故M的轨迹过坐标原点。

知识点

直接法求轨迹方程参数方程化成普通方程直线的参数方程圆的参数方程

继续学习学习下一知识点

下一知识点 : 椭圆的参数方程

百度题库 > 高考 > 文科数学 > 圆的参数方程

扫码查看完整答案与解析