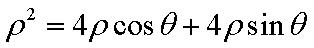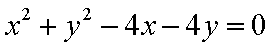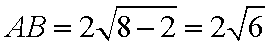- 极坐标系
- 共8题
1
题型:简答题
|
在极坐标系中,圆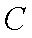
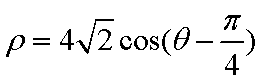
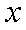
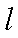
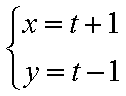
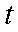

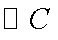
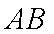
正确答案
见解析
解析
解: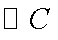
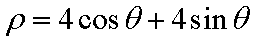

由
其圆心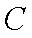
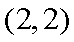

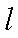
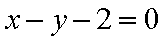
∴圆心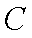
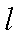
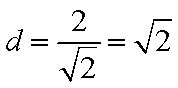
知识点
极坐标系
1
题型:简答题
|
在极坐标系中,A为曲线ρ2+2ρcosθ﹣3=0 上的动点,B为直线ρcosθ+ρsinθ﹣7=0 上的动点,求AB 的最小值。
正确答案
见解析
解析
由ρ2+2ρcosθ﹣3=0,得:x2+y2+2x﹣3=0,即(x+1)2+y2=4。
所以曲线是以(﹣1,0)为圆心,以2为半径的圆。
再由ρcosθ+ρsinθ﹣7=0得:x+y﹣7=0。
所以圆心到直线的距离为d=
则圆上的动点A到直线上的动点B的最小距离为
知识点
极坐标系
1
题型:简答题
|
在极坐标系中,已知直线




正确答案
见解析。
解析
直线的极坐标方程化为直角坐标方程为
圆的极坐标方程化为直角坐标方程为

因为截得的弦长为


即

知识点
极坐标系
下一知识点 : 简单曲线的极坐标方程
扫码查看完整答案与解析