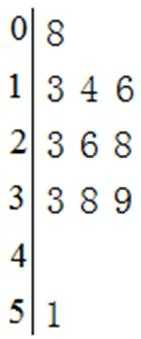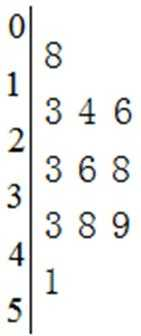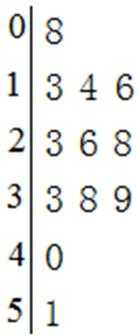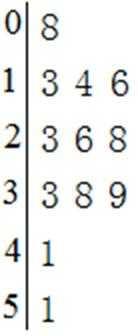- 频率分布直方图
- 共84题
4.数据8,51,33,39,38,23,26,28,13,16,14的茎叶图是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.某校从参加高一年级期中考试的学生中随机抽取



观察图形的信息,回答下列问题:
(Ⅰ)求分数在
(Ⅱ)用分层抽样的方法在分数段为




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 某城市要建成宜商、宜居的国际化新城,该城市的东城区、西城区分别引进8个厂家,现对两个区域的16个厂家进行评估,综合得分情况如茎叶图所示.
(Ⅰ)根据茎叶图判断哪个区域厂家的平均分较高;
(Ⅱ)规定85分以上(含85分)为优秀厂家,若从该两个区域各选一个优秀厂家,求得分差距不超过5的概率.
正确答案
(Ⅰ)东城区的平均分较高.
(Ⅱ)从两个区域各选一个优秀厂家,
则所有的基本事件共15种,
满足得分差距不超过5的事件(88,85)(88,85)(89,85)(89,94)(89,94)(93,94)(93,94)(94,,94)(94,,94)共9种.
所以满足条件的概率为
解析
解析已在路上飞奔,马上就到!
知识点
17.随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率。
正确答案
解:(1)由茎叶图知:设样本中甲班10位同学的平均身高为

则




(2)设甲班的样本方差为



(3)由茎叶图可知:
乙班这10名同学中身高不低于173cm的同学有5人,
身高分别为173cm、176cm、178cm、179cm、181cm.
这5名同学分别用字母A、B、C、D、E表示.
则记“随机抽取两名身高不低于173cm的同学”为事件Ω,则Ω包含的基本事件有:
[A,B]、[A,C]、[A,D]、[A,E]、[B,C]、[B,D]、[B,E]、[C,D]、[C,E]、[D,E]
共10个基本事件.
记“身高为176cm的同学被抽中”为事件M,
则M包含的基本事件为:[A,B]、[B,C]、[B,D]、[B,E]共4个基本事件.
由古典概型的概率计算公式可得:
解析
解析已在路上飞奔,马上就到!
知识点
18.从某学校的










(Ⅰ)求第七组的频率;
(Ⅱ)估计该校的


(Ⅲ)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他 们的身高分别为





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析