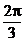正弦函数的单调性_章节学习

1

题型：填空题

|

填空题 · 5 分

13．在中，点，满足，．若，则；．

正确答案

解析

特殊化，不妨设，利用坐标法，以A为原点，AB为轴，为轴，建立直角坐标系，，，则，

.

考查方向

本题考查了平面向量基本定理的运用，一个向量用一组基底表示，存在唯一的实数对（x，y）使，向量等式成立．.

解题思路

本题考查平面向量的有关知识及及向量运算，利用向量相等条件求值，本题属于基础题.利用坐标运算要建立适当的之间坐标系，准确写出相关点的坐标、向量的坐标，利用向量相等，列方程组，解出未知数的值.

易错点

准确写出相关点的坐标、向量的坐标

知识点

正弦函数的单调性

1

题型：填空题

|

填空题 · 5 分

14.函数的图像可由函数的图像至少向右平移_____________个单位长度得到。

正确答案

知识点

正弦函数的单调性

1

题型：简答题

|

简答题 · 14 分

15．设函数的部分图象如图所示.

（1）求函数的解析式；

（2）当时，求的取值范围.

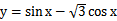
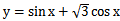
正确答案

（1）；

（2）

解析

试题分析：本题属于三角函数图像的基本问题，题目的难度是逐渐由易到难，（1）直接按照求A、ω、φ步骤来求（2）转化成求函数的最值，要结合图像，要特别注意函数的定义域。

（1）由图象知，，

又，，所以，得.

所以，将点代入，得，

即，又，所以.

所以.

（2）当时，，

所以，即.

考查方向

本题考查了三角函数的图形和性质，利用三角函数的图像求函数解析式，根据函数的图像求函数的取值范围。

解题思路

本题考查三角函数的图形和性质，解题步骤如下：

1、根据函数图像，确定A、ω、φ，进而求出函数的解析式。

2、求函数的解析式，必须在给定的x的取值范围内求解。

易错点

1、第一问中的根据角的范围如何确定φ。

2、第二问中求的取值范围，必须先求出x的取值范围，同时结合三角函数的图像去分析。

知识点

正弦函数的单调性由y=Asin（ωx+φ）的部分图象确定其解析式

1

题型：单选题

|

单选题 · 5 分

9．若函数f（x）＝4sinωx·＋cos2ωx（ω＞0）在[－，]上是增函数，则ω的取值范围是（）

A（0，1]

B（0，]

C[1，＋∞）

D[，＋∞）

正确答案

B

解析

由已知得：

是函数含原点的递增区间且函数在上递增，所以有即

因此A选项不正确，C选项不正确，D选项不正确，所以选B选项。

考查方向

本题主要考查了三角函数的诱导公式及单调性，在近几年的各省高考题出现的频率较高，常利用三角函数图像与性质求参数的取值范围来命题。

解题思路

先化简得,由f(x) 区间内单调递增可解得，因此A选项不正确，C选项不正确，D选项不正确，所以选B选项。

易错点

三角函数在某个给定区间递增或递减，不能正确转化满足条件的不等式。

知识点

正弦函数的单调性三角函数中的恒等变换应用

1

题型：单选题

|

单选题 · 5 分

7．函数f(x)＝sin(2x＋φ)的图像向左平移个单位后关于原点对称，则函数f(x)在区间上的最小值为(　　)

A

B

C

D

正确答案

A

解析

f(x)向右平移的函数记为g(x)= sin[2(x+)＋φ]= sin[2x+＋φ]，因为图像关于原点对称，所以g(x)为奇函数，φ=-，所以f(x)＝sin(2x - ) ,因为x0, ] , 2x - ,，由图象可知，最小值为－，选择答案A.

考查方向

三角函数图像的平移,对称问题,函数的单调性与最值问题。

解题思路

先平移，然后根据图像关于原点对称求解φ，再利用函数的单调性求最小值

易错点

1、本题易在左右平移时发生错误，易忽视x的系数；2、关于原点对称不理解；函数的基本性质理解不到位。

知识点

三角函数的周期性及其求法正弦函数的单调性

1

题型：简答题

|

简答题 · 12 分

16.已知向量，设

（I）求函数的解析式及单调增区间；

（II）在中，分别为内角A,B,C的对边，且，求的面积.

正确答案

（1）= []；

（2）

解析

试题分析：本题属于三角函数中的基本问题，题目的难度是逐渐由易到难，直接按照步骤来求

（Ⅰ）

=

由可得

所以函数的单调递增区间为[],

（Ⅱ）

由可得

考查方向

本题考查了利用三角函数的函数单调区间和解三角形求面积

解题思路

本题考查三角函数与解三角形，解题步骤如下：

1、利用向量的数量积求出并求出单调区间；

2、利用余弦定理求出，借助正弦定理求出面积

易错点

第一问中的辅助角容易计算错误

知识点

正弦函数的单调性三角函数中的恒等变换应用正弦定理余弦定理平面向量数量积的运算

1

题型：单选题

|

单选题 · 5 分

4.使函数是奇函数，且在上是减函数的的一个值是（）

A

B

C

D

正确答案

B

解析

考查方向

本题主要考察了求函数y＝Asin(x＋)的解析式，考察了正弦函数的奇偶性，考察了特殊角的三角函数值求解，主要考察学生对三角函数的图像及性质的理解，本题较简单

解题思路

1、通过和角公式求函数y＝Asin(x＋)的解析式，

2、利用函数奇偶性以及在上为减，确定在原点处对称中心为减区间上的零点得出关于的关系，

3，根据选项得出结果

易错点

本题易于在求解时，单调性的作用

知识点

正弦函数的单调性函数y＝Asin(ωx＋φ)的应用

1

题型：简答题

|

单选题

在古代，黄河流域的自然环境是很优越的。那时，这里的气候温暖湿润，土地肥沃，到处是青山绿野，植物种类繁多，为原始人类的生存提供了有利的条件。殷代以后黄河中下游流域成为我国开发最早的地区，经济发展、人口繁衍较快，政治、文化也比较先进。因此，黄河流域成为中华民族成长的摇篮。下列不是“黄河流域成为中华民族成长的摇篮”的自然原因的一项是( )。

A．经济发展，人口繁衍较快
B．气候温暖湿润
C．植物种类繁多，食物丰富
D．土地肥沃，到处是青山绿野

正确答案

A

解析

[解析] B、C、D三项都是“黄河流域成为中华民族成长的摇篮”的自然原因，而A项是人类社会形成后的状况。所以本题答案为A。

1

题型：单选题

|

单选题 · 5 分

一排9个座位坐了3个三口之家，若每家人坐在一起，则不同的坐法种数为

A3×3！

B3×(3！)3

C(3！)4

D9！

正确答案

C

解析

此排列可分两步进行，先把三个家庭分别排列，每个家庭有种排法，三个家庭共有种排法；再把三个家庭进行全排列有种排法。因此不同的坐法种数为，答案为C

知识点

正弦函数的单调性

1

题型：填空题

|

填空题 · 5 分

B【分析】由于题设条件含有抽象函数，本题最简便的方法是用赋值法求解，即取符合题设条件的特殊函数去计算，然后选择正确选项.

【详解】取

.

则当时，，

而，所以为连续的偶函数，则选项（Ｂ）正确，故选（Ｂ）.

【评注】对于题设条件含抽象函数或备选项为抽象函数形式结果以及数值型结果的选择题，用赋值法求解往往能收到奇效.

符合题设条件的函数在多教科书上均可见到，完全类似例题见2006文登最新模拟试卷（数学三）（8）.

正确答案

B【分析】由于题设条件含有抽象函数，本题最简便的方法是用赋值法求解，即取符合题设条件的特殊函数去计算，然后选择正确选项.

【详解】取

.

则当时，，

而，所以为连续的偶函数，则选项（Ｂ）正确，故选（Ｂ）.

【评注】对于题设条件含抽象函数或备选项为抽象函数形式结果以及数值型结果的选择题，用赋值法求解往往能收到奇效.

符合题设条件的函数在多教科书上均可见到，完全类似例题见2006文登最新模拟试卷（数学三）（8）.

知识点

正弦函数的单调性

热门试卷

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

正确答案

解析

知识点

正确答案

知识点