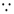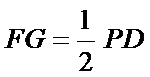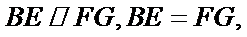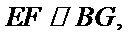- 棱柱、棱锥、棱台的体积
- 共170题
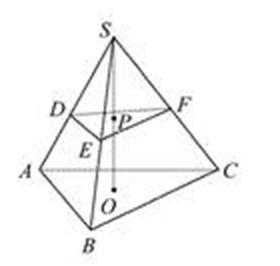
14.在三棱锥S—ABC内任取一
正确答案
解析
如图所示,只有当P点为SO的中点,即当P在三棱锥的中截面与下底面构成的三棱台内时,符合要求。所以填
考查方向
概率、三棱锥的体积的求法。
解题思路
根据题意做出图形,求解
易错点
不会计算三棱锥体积,不理解相关概率的意义
知识点
19.已知在四棱锥S—ABCD中,底面ABCD是平行四边形,若SB丄AC,SA = SC.(1)求证:平面SBD丄平面(2)若 AB = 2,SB = 3,cos∠SCB=
正确答案
如图所示
因为SA=SC,
所以SO∩SB=S,
所以AC⊥平面SBD,
因为AC在平面ABCD内,
所以平面SBD⊥平面ABCD
(2)⊥平面ABCD,即
由(1)知,AC⊥BD,所以底面ABCD是菱形,
所以BC=AB=2
因为SB=3,cos∠SCB=1/8
所以由余弦定理可得,SC=2,
所以∠SAC=60°,
所以SAC是等边三角形
所以在Rt△SOH中,SH=SO*sin60°=3/2
所以
解析
证AC垂直于面ABCD, 设AC交BD于0,因为SA=SC,SO交SB于S,所以AC垂直于平面SBD,因为AC在平面ABCD内,所以面SBD垂直于面ABCD.求底面面积时,先用余弦定理求出角SOB=120度,角SOH=60度,所以四棱锥的体积为
考查方向
立体几何中的相关计算和证明
解题思路
通过线线垂直得到线面垂直,进而得到面面垂直,找清四棱锥的底面和高,利用公式求解。
易错点
面面垂直概念混淆,立体感不强
知识点
10.点A,B,C,D在同一个球的球面上,AB = B


正确答案
解析
AB=BC=AC=√3∴四面体ABCD体积最大时,D在ABC的另一个半球内正△ABC面积=3√3/4∴高=4∴D到面ABC距离=4ABC所在面的圆心为O'球心为O∴O'A=O'B=O'C=2√3×√3×sin60°=1设球的半径为R勾股定理得(4-R)²+1²=R²解得R=17/8∴表面积=4πR²=289/16
考查方向
本题主要与球体有关的计算、四面体体积最值问题。属于较难题
解题思路
先找到四面体体积最大时球的半径,然后再求表面积
易错点
找不到四面体体积最大时的情况,忘记球表面积计算公式
知识点
6.若正三棱柱的所有棱长均为


正确答案
4
解析
若正三棱柱的所有棱长均为
则其体积为
由

知识点
9.右图是一个四面体的三视图,这三个视图均是腰长为2的等腰直角三角形,正视图和俯视图中的虚线是三角形的中线,则该四面体的体积为
正确答案
解析
由图可知,此几何体为底边长分别为1,2,高为2的三棱锥。B选项不正确,C选项不正确,D选项不正确,所以选A选项。本题主要考查三视图
考查方向
本题主要考查三视图
解题思路
1、还原几何体;
2、求出体积,即可得到结果。B选项不正确,C选项不正确,D选项不正确,所以选A选项。
易错点
本题易在还原几何体时发生错误。
知识点
19.如图,矩形CDEF和梯形ABCD互相垂直,∠BAD=∠ADC=90°,AB=AD=
正确答案
(1)略;(2)
解析
⑴证明:设






因为

所以

又因为



所以

⑵解:取









所以

同理

所以,



所以四边形

所以

又因为

所以
又

所以


注意到


所以
考查方向
本题考查了立体几何中的线面平行和体积.属于考中的高频考点。
解题思路
本题考查立体几何,解题步骤如下:
1、转化为证明线线平行。
2、利用体积公式求解。
易错点
第一问中的线面平行的转化。
知识点
19.(本小题满分12分)如图,已知四棱锥


(Ⅰ)证明:
(Ⅱ)若

正确答案
见解析
解析
(Ⅰ)
证明:取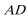





又






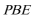

(Ⅱ)
由(Ⅰ)






由侧面





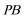
考查方向
解题思路
作出适当的辅助线,根据线面垂直证明线线垂直
易错点
找垂直条件时找不到
知识点
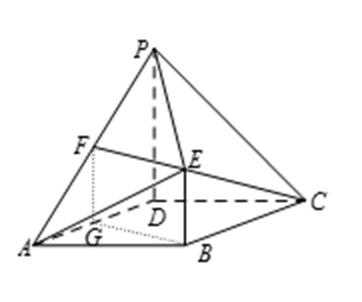
18. 如图,四边形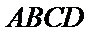
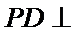
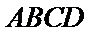
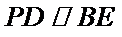
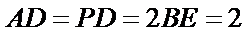
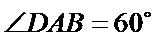
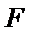
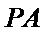
(Ⅰ)求证: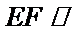
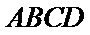
(Ⅱ)求证:平面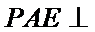
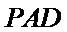
(Ⅲ)求三棱锥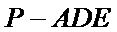
正确答案
(Ⅰ)略;
(Ⅱ)略;
(Ⅲ)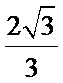
解析
(Ⅰ)取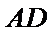
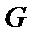
因为点
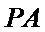
所以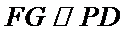
又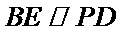
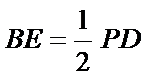
所以
所以四边形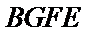
所以
又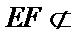
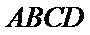
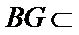
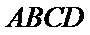
所以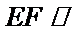
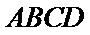
(Ⅱ)连接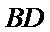
因为四边形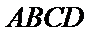
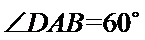

因为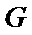
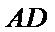
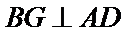
又因为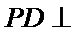
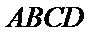
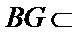
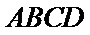
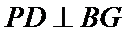
又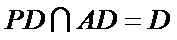
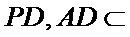
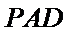
所以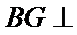
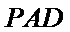
又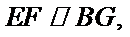
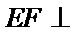
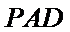
又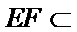
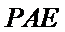
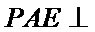
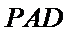
法二:因为四边形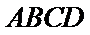
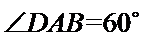
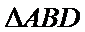
因为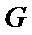
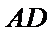
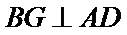
又因为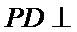
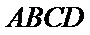
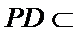
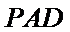
所以平面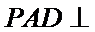
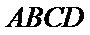
又平面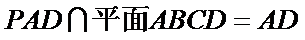
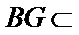
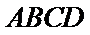
所以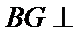
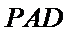
又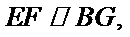
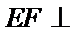
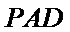
又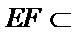
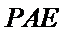
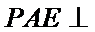

(Ⅲ)因为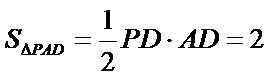
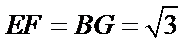
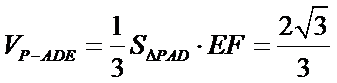
考查方向
本题考查了线面平行,面面垂直的证明,体积的求法,在近几年的各省高考题出现的频率非常高.
解题思路
(Ⅰ)借助于平行四边形,得到线线平行,进而得到线面平行;
(Ⅱ)利用面面垂直的判定定理;
易错点
定理记忆不清致误.
知识点





正确答案
考查方向
易错点
本题容易在没有发现B,D点的位置关系,导致无法解答
知识点
11. 某三棱柱的三视图如图所示,则该三棱柱的体积为
正确答案
4
解析
如图,画出三棱柱,可知体积
考查方向
本题考查了通过三视图还原实物的能力,在近几年的各省高考题出现的频率非常高.
解题思路
由三视图可知三棱柱的一个侧面是水平放置的.
易错点
不能还原出实物图像.
知识点
扫码查看完整答案与解析