- 棱柱、棱锥、棱台的体积
- 共170题
6.若正三棱柱的所有棱长均为


正确答案
4
解析
依题意,

考查方向
解题思路
简单几何体的表面积和体积计算是高考的一个常见考点,解决这类问题,首先要熟练掌握各类简单几何体的表面积和体积计算公式,其次要掌握平几面积计算方法.柱的体积为



易错点
准确计算
知识点
19.如图,圆锥的顶点为










正确答案
解析
试题分析:因为

所以三棱锥

因为




在


过


在

所以异面直线


考查方向
解题思路
求异面直线所成的角常采用“平移线段法”,平移的方法一般有三种类型:利用图中已有的平行线平移;利用特殊点(线段的端点或中点)作平行线平移;补形平移.计算异面直线所成的角通常放在三角形中进行.
易错点
异面直线所成角的寻找
知识点
如图1,在直角梯形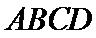


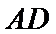
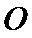


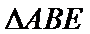
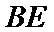
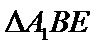

19.证明: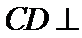
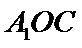
20.当平面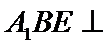
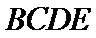
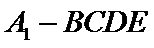

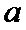
正确答案
(Ⅰ) 略.
解析
试题分析: (Ⅰ) 在图1中,因为

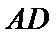
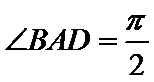
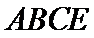
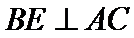
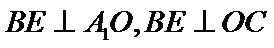
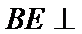
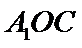
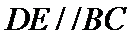

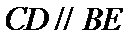
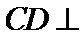
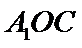
(Ⅰ)在图1中,因为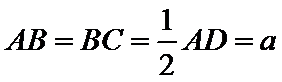
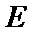
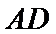

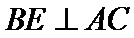
即在图2中,
从而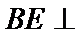
又
所以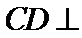
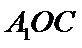
考查方向
解题思路
在处理有关空间中的线面平行.线面垂直等问题时,常常借助于相关的判定定理来解题,同时注意恰当的将问题进行转化
易错点
线线关系与线面关系的转换
正确答案
(Ⅱ) 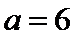
解析
试题分析:(Ⅱ)由已知,平面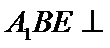
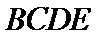

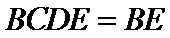
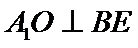
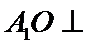
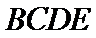
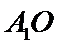
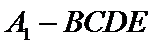
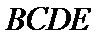
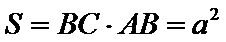
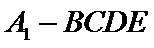
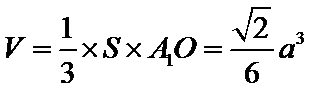
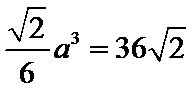
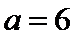
(Ⅱ)由已知,平面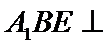
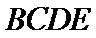
且平面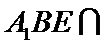
又由(Ⅰ)知,
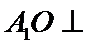
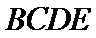
即
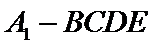
由图1可知,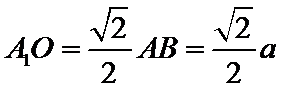
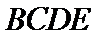
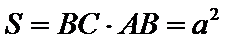
从而四棱锥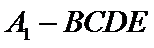
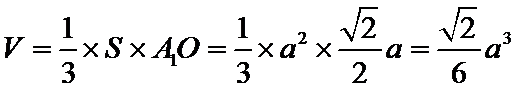
由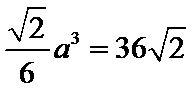
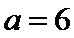
考查方向
解题思路
2.求几何体的体积的方法主要有公式法.割补法.等价转化法等,本题是求四棱锥的体积,可以接使用公式法.
易错点
体积的计算
8.设一个正方体与底面边长为

正确答案
解析
设正方体的棱长为a,利用等体积法即可计算出正方体的棱长为a=
考查方向
本题主要考查了空间几何体的体积计算及空间想象能力,体现了学生的基础知识掌握能力。
解题思路
空间几何体的体积计算及空间想象能力
易错点
对几何体的体积计算公式理解不到位,使用错公式。
知识点
19.如图,直三棱柱





(1)证明:平面
(2)平面
正确答案
(1)见解析;(2)3:2.或2:3
解析
试题分析:本题属于立体几何的证明和体积的求解问题,(1)要证明面面垂直,只要证明线面垂直,而线面垂直又最终转化为证明线线垂直;(2)分别计算2个几何体的体积即可。
(1)由题意 



又




(2)设棱锥




所以
考查方向
解题思路
本题考查立体几何的证明和体积的求解问题,解题步骤如下:(1)要证明面面垂直,只要证明线面垂直,而线面垂直又最终转化为证明线线垂直;(2)分别计算2个几何体的体积即可。
易错点
不熟练面面垂直的判定定理。
知识点
8. 三棱锥P-ABC的三条侧棱两两垂直,三个侧面的面积分别是


正确答案
解析
因为三条侧棱两两垂直,所以可设



考查方向
解题思路
三棱锥的外接球实际上是它扩展为长方体的外接球,求长方体的对角线的长,就是球的直径,然后求球的体积
易错点
立体感不强;计算能力弱
知识点
16.在正三棱锥V—ABC内,有一半球,其底面与正三棱锥的底面重合,且与正三棱锥的三个侧面都相切,若半球的半径为2,
正确答案
解析
设球心为O,设底边OD=x和体高OP=x,如图:则
考查方向
解题思路
1)设底边长a和侧高l
2)把三棱锥的体积分割成以球心为定点的三个三棱锥,求体积之和即椎体的体积
3)根据体积求出a.l的关系
4)利用公式计算体高
易错点
主要易错于球的几何性质用错
知识点
6.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺。问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧度为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放斛的米约有( )
正确答案
知识点
19. 如图,在三棱锥P-AMC中,AC=AM=PM=2,PM⊥面AMC,AM⊥AC,B,D分别为CM,AC的中点.
(Ⅰ)在PC上确定一点E,使得直线PM∥平面ABE,并说明理由;
(Ⅱ)在(Ⅰ)的条件下,连接AE,与PD相交于点N,求三棱锥B-ADN的体积.
正确答案
(1)E为PC的中点;(2)
解析
试题分析:本题属于立体几何证明与求体积的问题,(1)利用线面垂直的判定定理来证明;(2)将体积最终转化为
(Ⅰ)E为PC的中点.理由如下:
连接BE,由于B,E分别为CM,PC的中点,
所以BE∥PM,
又BE

所以PM∥面ABE.
(Ⅱ)由于AE,PD分别是△PAC的边PC,AC上的中线,所以AE和PD的交点N为△PAC的重心,故N为PD靠近D的三等分点,
则
而因为D为AC的中点,所以
又由于E为PC的中点,
所以
所以三棱锥B-AND的体积为
考查方向
解题思路
本题考查立体几何证明与求体积的问题,解题步骤如下:
(1)利用线面垂直的判定定理来证明;
(2)将体积最终转化为
易错点
求体积的时候不会转化。
知识点
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,
21.求证:AD⊥平面BFED;
22.已知点P在线段EF上,
正确答案
见解析
解析
(1)在梯形
∵

∴
∴


平面

∴
∴
∴
考查方向
解题思路
该题解题关键在于找到所求内容的突破点
1)根据余弦定理得出BD进而推出
2)由面面垂直得到线面垂直
3)确定PE为体高,进而求出体积
易错点
本题容易在
正确答案
见解析
解析
解:
(2)由(1)知
∵


∴
考查方向
解题思路
该题解题关键在于找到所求内容的突破点
1)根据余弦定理得出BD进而推出
2)由面面垂直得到线面垂直
3)确定PE为体高,进而求出体积
易错点
本题容易在
扫码查看完整答案与解析