- 补集及其运算
- 共55题
1.设集合

正确答案
解析
试题分析:因为

考查方向
解题思路
先分别求出两个集合中代表元素的取值范围,再求交集。
易错点
对一元二次不等式不熟悉导致出错。
知识点
1.设全集



正确答案
解析
因为
考查方向
解题思路
研究两集合的关系时,关键是将两集合的关系转化为元素间的关系,本题实质求满足属于集合A或不属于集合B的元素的集合.
易错点
研究集合问题,一定要抓住元素,看元素应满足的属性.
知识点
1.已知全集



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.若全集
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.若集合A={x|ax2-ax+1<0}=⌀,则实数a的取值范围是( )
正确答案
解析
由题意知,当a=0时,满足条件.
当a≠0时,
由得0<a≤4.综上所述,
得0≤a≤4.
知识点
1.集合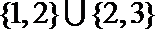
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知全集U=R,集合A={x|x<一1或x>4},B={x|-2≤x≤3},那么阴影部分表示的集合为()
正确答案
解析
由韦恩图可知阴影部分表示的集合为
又集合A={x|x<一1或x>4)}={X| 
所以
考查方向
解题思路
1、由韦恩图可知阴影部分表示的集合为
2、集合A={x|x<一1或x>4)}={X| 
易错点
本题易在观察韦恩图时发生错误,易忽视补集的运算。
知识点
1.已知全集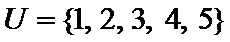
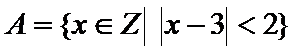
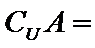
正确答案
解析
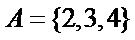
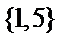
考查方向
解题思路
先求出集合A,然后根据补集的定义求出相应的结果。
易错点
本题容易因为不能准确理解补集的含义而导致错误。
知识点
2.已知全集U=R,集合

正确答案
解析
画出数轴,标出集合A的取值范围,由补集的概念,取其不包含的范围即可得出结论。
一定要注意端点的取舍,包含端点用实心点,不包含端点用空心点。
考查方向
解题思路
本题主要考查了子、交、并、补的运算,用数轴法来做形象直观,不易出错。
易错点
本题必须注意端点的取舍,忽视则会出现错误。
知识点
2.已知全集U=R,集合

正确答案
解析
∵




考查方向
本题主要考查了集合的补集运算以及分式不等式的解法,考查学生基础知识的掌握能力,在近几年的各省高考题出现的频率较高,常与一元二次不等式、分式不等式、绝对值不等式、指数不等式、对数不等式的求解等知识点交汇命题.属于容易题,也属于易错题.
解题思路
先化简集合




易错点
1.分式不等式转化为整式不等式求解时要考虑分母不为零的情况;
2.求一个集合的补集时,要注意“

知识点
扫码查看完整答案与解析