利用基本不等式求最值
共109题

· 利用基本不等式求最值

利用基本不等式求最值
共109题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

题型：简答题

简答题 · 14 分

为了保护环境，某工厂在国家的号召下，把废弃物回收转化为某种产品，经测算，处理成本（万元）与处理量（吨）之间的函数关系可近似的表示为：，且每处理一吨废弃物可得价值为万元的某种产品，同时获得国家补贴万元。

（1）当时，判断该项举措能否获利？如果能获利，求出最大利润；如果不能获利，请求出国家最少补贴多少万元，该工厂才不会亏损？

（2）当处理量为多少吨时，每吨的平均处理成本最少？

正确答案

见解析

解析

（1）根据题意得，利润和处理量之间的关系：

，.

∵，在上为增函数，

可求得

∴ 国家只需要补贴万元，该工厂就不会亏损。

（2）设平均处理成本为

，

当且仅当时等号成立，由得。

因此，当处理量为吨时，每吨的处理成本最少为万元。

知识点

利用基本不等式求最值

题型：简答题

简答题 · 16 分

阅读：

应用上述解法，求解下列问题：

（1）已知，，求的最小值；

（2）已知，求函数的最小值；

（3）已知正数、、，，

求证：.

正确答案

见解析

解析

（1），

而，

当且仅当时取到等号，则，即的最小值为.

（2），

而，，

当且仅当，即时取到等号，则，

所以函数的最小值为.

（3）

当且仅当时取到等号，则.

知识点

利用基本不等式求最值类比推理

题型：填空题

填空题 · 4 分

已知当mn取得最小值时，直线与曲线的交点个数为

正确答案

解析

略

知识点

利用基本不等式求最值直线与圆锥曲线的综合问题

题型：单选题

单选题 · 5 分

若，则的取值范围是（）

正确答案

解析

本题考查的是均值不等式，因为，即，所以，当且仅当，即时取等号。

知识点

利用基本不等式求最值

题型：填空题

填空题 · 4 分

已知实数满足，，则的最大值是____________；

正确答案

解析

因为，所以，所以，

所以，故实数的最大值为.

知识点

利用基本不等式求最值

题型：填空题

填空题 · 4 分

已知，则的最小值为_____________.

正确答案

解析

(探究性理解水平/基本不等式)

由题：=1,所以xy=2,由基本不等式得：2=xy,则8，所以

x+yx+y的最小值为

知识点

对数的运算性质利用基本不等式求最值

题型：填空题

填空题 · 4 分

已知，且满足，则xy的最大值为 .

正确答案

解析

略。

知识点

利用基本不等式求最值

题型：简答题

简答题 · 18 分

函数的定义域为，若存在常数，使得对一切实数均成立，则称为“圆锥托底型”函数。

（1）判断函数，是否为“圆锥托底型”函数？并说明理由。

（2）若是“圆锥托底型” 函数，求出的最大值。

（3）问实数、满足什么条件，是“圆锥托底型” 函数。

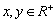
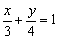
正确答案

见解析

解析

（1）。，即对于一切实数使得成立，“圆锥托底型” 函数。

对于，如果存在满足，而当时，由，，得，矛盾，不是“圆锥托底型” 函数。

（2）是“圆锥托底型” 函数，故存在，使得对于任意实数恒成立。

当时，，此时当时，取得最小值2，。

而当时，也成立。

的最大值等于。

（3）①当，时，，无论取何正数，取，则有，

不是“圆锥托底型” 函数。

②当，时，，对于任意有，此时可取是“圆锥托底型” 函数。

③当，时，，无论取何正数，取，有，不是“圆锥托底型” 函数。

④当，时，，无论取何正数，取，有，不是“圆锥托底型” 函数。

由上可得，仅当时，是“圆锥托底型” 函数

知识点

求函数的值利用基本不等式求最值

题型：填空题

填空题 · 5 分

在如图所示的锐角三角形空地中, 欲建一个面积最大的内接矩形花园(阴影部分), 则其边长x为（） (m)。

正确答案

解析

利用均值不等式解决应用问题。设矩形高为y, 由三角形相似得:

知识点

利用基本不等式求最值基本不等式的实际应用

继续学习学习下一知识点

下一知识点 : 不等式与函数的综合问题

百度题库 > 高考 > 文科数学 > 利用基本不等式求最值

扫码查看完整答案与解析