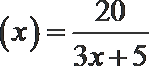- 利用基本不等式求最值
- 共109题
1
题型:
单选题
|
18.对于使






正确答案
D
解析
解析已在路上飞奔,马上就到!
知识点
函数的最值利用基本不等式求最值
1
题型:填空题
|
13.若两个正实数



正确答案
8
解析
解析已在路上飞奔,马上就到!
知识点
利用基本不等式求最值
1
题型:简答题
|
20.我国发射的天宫一号飞行器需要建造隔热层.已知天宫一号建造的隔热层必须使用20年,每厘米厚的隔热层建造成本是3万元,天宫一号每年的能源消耗费用C(万元)与隔热层厚度

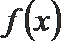
(1)求
(2)当隔热层修建多少厘米厚时,总费用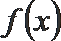
正确答案
(1)当
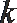
(2)
当且仅当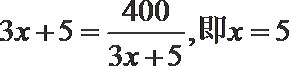
即隔热层修建5厘米厚时,总费用达到最小值,最小值为35万元.
解析
解析已在路上飞奔,马上就到!
知识点
函数模型的选择与应用利用基本不等式求最值
1
题型:
单选题
|
9.若正数


正确答案
A
解析
解析已在路上飞奔,马上就到!
知识点
利用基本不等式求最值
1
题型:简答题
|
20.为了提高产品的年产量,某企业拟在2014年进行技术改革,经调查测算,产品当年的产量




(1)试确定


(2)该企业2014年的技术改革费用投入多少万元时,厂家的利润最大?并求出最大利润.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
函数模型的选择与应用利用基本不等式求最值
下一知识点 : 不等式与函数的综合问题
扫码查看完整答案与解析