热门试卷

（1）由方程得判别式

因为,所以

当时,,此时,所以；

当时,,此时,所以；

当时,,设方程的两根为且,

则 ,,

当时,,,所以

此时,

当时,,所以

此时,.

综上,

（2） ,

所以函数在区间上为减函数,在区间和上为增函数

当时,因为,所以在内的极值点为；

当时,,所以在内有极大值点；

当时,

由,很容易得到

（可以用作差法，也可以用分析法）,所以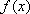在内有极大值点；

当时,

由,很容易得到,此时在,内没有极值点。

综上,当时,极值点为；当时,极值点为；当时,无极值点。

（1）设BD=x，则CD=3﹣x

∵∠ACB=45°，AD⊥BC，∴AD=CD=3﹣x

∵折起前AD⊥BC，∴折起后AD⊥BD，AD⊥CD，BD∩DC=D

∴AD⊥平面BCD

∴VA﹣BCD=×AD×S△BCD=×（3﹣x）××x（3﹣x）=（x3﹣6x2+9x）

设f（x）=（x3﹣6x2+9x）  x∈（0，3），

∵f′（x）=（x﹣1）（x﹣3），∴f（x）在（0，1）上为增函数，在（1，3）上为减函数

∴当x=1时，函数f（x）取最大值

∴当BD=1时，三棱锥A﹣BCD的体积最大；

（2）以D为原点，建立如图直角坐标系D﹣xyz，

由（1）知，三棱锥A﹣BCD的体积最大时，BD=1，AD=CD=2

∴D（0，0，0），B（1，0，0），C（0，2，0），A（0，0，2），M（0，1，1），E（，1，0），且=（﹣1，1，1）

设N（0，λ，0），则=（﹣，λ﹣1，0）

∵EN⊥BM，∴•=0

即（﹣1，1，1）•（﹣，λ﹣1，0）=+λ﹣1=0，∴λ=，∴N（0，，0）

∴当DN=时，EN⊥BM

设平面BMN的一个法向量为=（x，y，z），由及=（﹣1，，0）

得，取=（1，2，﹣1）

设EN与平面BMN所成角为θ，则=（﹣，，0）

sinθ=|cos＜，＞|=||==

∴θ=60°

∴EN与平面BMN所成角的大小为60°