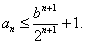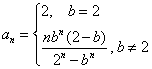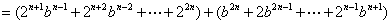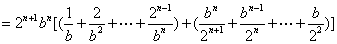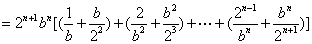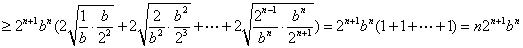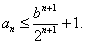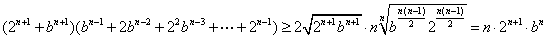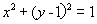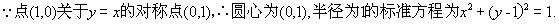3．已知单位向量
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3．在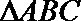
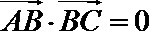
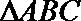
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
将函数
A
B
C
D
正确答案
解析
将函数
再把所得各点的横坐标伸长到原来的2倍（纵坐标不变），所得图像的函数解析式是
知识点
设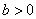
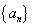
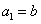
（1）求数列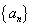
（2）证明：对于一切正整数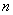
正确答案
见解析
解析
（1）由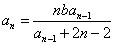
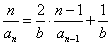
当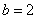
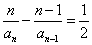
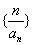
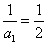
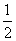
所以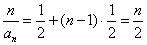
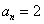
当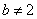
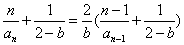
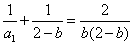
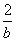
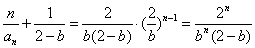
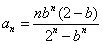
综上所述,数列
（2）当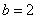
当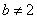
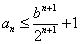
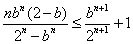
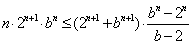
因为
所以不等式（*）成立，从而原不等式成立；
综上所述，当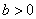
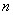
(解后反思)事实上如果利用多元基本不等式更简单,
知识点
要制作一个容器为4m3，高为1m的无盖长方形容器，已知该容器的底面造价是每平方米20元，侧面造价是每平方米10元，则该容器的最低总造价是 （单位：元）
正确答案
160
解析
不等式的解法及应用。
此题首先需要由实际问题向数学问题转化，设池底长和宽分别为a，b，成本为y，建立函数关系式，然后利用基本不等式求出最值即可求出所求。
设池底长和宽分别为a，b，成本为y，
则长方形容器的容器为4m3，高为1m，
故底面面积S=ab=4，y=20S+10[2（a+b）]=20（a+b）+80，
a+b≥2
故当a=b=2时，y取最小值160，
即该容器的最低总造价是160元
知识点
设
正确答案
解析
知识点
若圆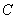
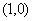
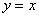
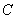
正确答案
解析
知识点
已知集合
A
B
C
D
正确答案
解析
略
知识点
扫码查看完整答案与解析