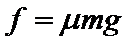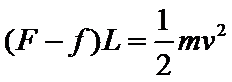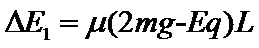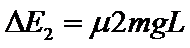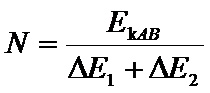- 动量守恒定律
- 共299题
在光滑绝缘水平面上方某区域(X≤3L)有沿x轴正方向的水平匀强电场,电场强度的大小及分布情况如图1所示。将质量为m1、电荷量为+q的带电小球A在x=0处由静止释放,小球A将与质量为m2、静止于x=L处的不带电的绝缘小球B发生正碰。已知两球均可视为质点,碰撞时间极短,且碰撞过程中没有机械能的损失,没有电荷量的转移。 E0、L为已知。
图一
图二
33.若
a.两小球第一次碰撞前,小球A运动的时间t0以及碰撞前瞬时的速度大小v0;
b.在图2中画出小球A自x=0处运动到x=5L处过程中的v-t图像。
34.若
正确答案
a.小球A与小球B碰撞前瞬时速度
b.v-t图像如答图所示
解析
a.小球A第一次与小球B碰撞前做初速度为零的匀加速直线运动
加速度
运动时间
小球A与小球B碰撞前瞬时速度
b.小球A自x=0处运动到x=5L处的过程中的v-t图像如答图所示
考查方向
牛顿第二定律; 匀变速直线运动的公式
解题思路
a、小球A第一次与小球B碰撞前做初速度为零的匀加速直线运动,由牛顿第二定律和位移公式结合求出时间,再由速度公式求碰撞前瞬时的速度.
b、根据速度与时间的关系,画出v-t图象.
易错点
本题关键对带电小球进行受力分析,利用牛顿第二定律求出加速度.
正确答案
无论倍数k取何值,小球A均可与小球B发生第二次碰撞。
解析
设两小球第一次碰撞后速度分别为vA1、vB1.
取碰撞前A球的速度方向为正方向,由动量守恒定律得:
km2v0=km2vA1+m2vB1;
由机械能守恒定律得:
解得 :


解得 :
则 vA2>vB1所以无论倍数k取何值,小球A均可与小球B发生第二次碰撞.
考查方向
动量守恒定律;功能关系
解题思路
碰撞过程中没有机械能的损失,根据动量守恒定律和能量机械能守恒定律结合求出碰后两球的速度表达式.碰后A球再次被电场加速,结合动能定理和能发生第二次碰撞的条件解答.
易错点
由于动量是矢量,注意使用动量守恒定律解题时要规定正方向.
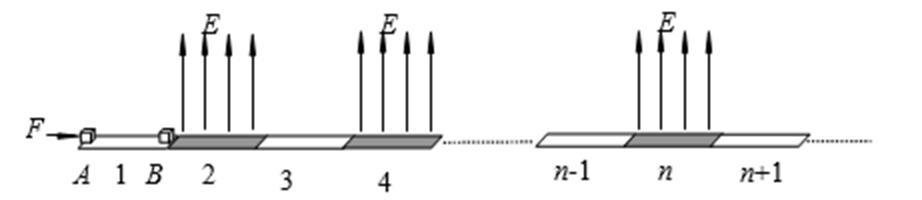
如图所示,有一固定在水平面的平直轨道,该轨道由白色轨道和黑色轨道交替排列并平滑连接而成。各段轨道的编号已在图中标出。仅黑色轨道处在竖直向上的匀强电场中,一不带电的小滑块A静止在第1段轨道的最左端,绝缘带电小滑块B静止在第1段轨道的最右端。某时刻给小滑块A施加一水平向右的恒力F,使其从静止开始沿轨道向右运动,小滑块A运动到与小滑块B碰撞前瞬间撤去小滑块A所
18.求F的大小;
19.碰撞过程中滑块B对滑块A的冲量;
20.若A和B最终停在轨道上编号为k的一段,求k的数值。
正确答案
以滑块A为研究对象,
在第1段轨道上,滑块A受到摩擦力的大小
对于滑块A在第1段轨道上从最左端到最右端的过程,
根据动能定理有
解得:F=1.84N
解析
以滑块A为研究对象,
在第1段轨道上,滑块A受到摩擦力的大小
对于滑块A在第1段轨道上从最左端到最右端的过程,
根据动能定理有
解得:F=1.84N
考查方向
动能定理
解题思路
对于滑块A在第1段轨道上从最左端到最右端的过程,由动能定理求解。
易错点
利用动能定理时一定要选择好对哪个阶段列方程
正确答案
设滑块A、B碰撞后瞬间A和B的共同速度为vAB,根据动量守恒定律有
mv=2m vAB
设滑块B对滑块A的冲量为I, 规定水平向右为正方向。
以滑块A为研究对象,根据动量定理有:I =mv AB-mv,
解得:I=-0.030N•s
滑块B对滑块A冲量的方向水平向左
解析
设滑块A、B碰撞后瞬间A和B的共同速度为vAB,根据动量守恒定律有
mv=2m vAB
设滑块B对滑块A的冲量为I, 规定水平向右为正方向。
以滑块A为研究对象,根据动量定理有:I =mv AB-mv,
解得:I=-0.030N•s
滑块B对滑块A冲量的方向水平向左
考查方向
动量守恒定律和动量定理
解题思路
由动量守恒定律求出共同速度,然后由动量定理计算冲量
易错点
动量守恒定律是矢量式,要考虑方向
正确答案
设滑块A和B每经过一段长为L的黑色轨道损失的动能为ΔE1,则
设滑块A和B每经过一段长为L的白色轨道,损失的动能为ΔE2,则
设滑块A和B碰撞后瞬间的总动能为EkAB,令
解得:N=7.5
即滑块通过标号为15的白色轨道后,仍有动能Ek=0.5(ΔE1+ΔE2) =6×10-3J,
因Ek>ΔE1,故物块可通过第16号轨道而进入第17号轨道,
进入第17号轨道时的动能Ek′= Ek-ΔE1=2×10-3J< ΔE2,故将不能通过第17号轨道,即最终停在第17号轨道上。
解析
设滑块A和B每经过一段长为L的黑色轨道损失的动能为ΔE1,则
设滑块A和B每经过一段长为L的白色轨道,损失的动能为ΔE2,则
设滑块A和B碰撞后瞬间的总动能为EkAB,令
解得:N=7.5
即滑块通过标号为15的白色轨道后,仍有动能Ek=0.5(ΔE1+ΔE2) =6×10-3J,
因Ek>ΔE1,故物块可通过第16号轨道而进入第17号轨道,
进入第17号轨道时的动能Ek′= Ek-ΔE1=2×10-3J< ΔE2,故将不能通过第17号轨道,即最终停在第17号轨道上。
考查方向
功能关系和数学知识的结合
解题思路
由功能关系计算出损失的能量,然后根据数学知识求出K
易错点
对常见的功能关系不熟悉
17.如图所示,固定点O上系一长L = 0.5 m的轻细绳,细绳的下端系一质量m = 1.0 kg的小球(可视为质点),原来处于静止状态,球与平台的B点接触无压力,平台高h = 0.80 m,一质量M = 2.0 kg的物块开始静止在平台上的P点,现对物块施予一水平向右的初速度V0,物块沿粗糙平台自左向右运动到平台边缘B处与小球发生正碰,碰后小球在绳的约束下做圆周运动,恰好能通过最高点A,而物块落在水平地面上的C点,其水平位移S=1.0 m,不计空气阻力,g =10 m/s2 ,求:
(1)求物块碰撞后的速度;
(2)若平台表面与物块间动摩擦因数μ=0.5,物块与小球的初始距离为S1=1.5 m,物块在P处的初速度大小为多少?
正确答案
(1)V=2.5 m/s;
(2)
解析
(1)碰后物块M做平抛运动,设其平抛运动的初速度为V


(2)物块与小球在B处碰撞,设碰撞前物块的速度为V1,碰撞后小球的速度为V2,
由动量守恒定律: MV1 = mV2 + MV
碰后小球从B处运动到最高点A过程中机械能守恒,设小球在A点的速度为VA:
小球在最高点时依题给条件有:
物块M从P运动到B处过程中,由动能定理:
解得:

考查方向
解题思路
(1)平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据水平方向上和竖直方向上的运动规律求出质量为M的物块落地时的速度大小。
(2)根据牛顿第二定律和机械能守恒定律求出碰撞后B球的速度,根据平抛运动得出M碰后的速度,结合动量守恒定律求出碰撞前M到达B点的速度,根据动能定理求出物块M在P处的初速度大小。
易错点
非弹性碰撞,动量守恒定律,机械能不守恒。
知识点
37.选做题三
在一水平支架上放置一个质量m1=0.98kg的小球A,一颗质量为m0=20g的子弹以水平初速度V0=400m/s的速度击中小球A并留在其中。之后小球A水平抛出恰好落入迎面驶来的沙车中,已知沙车的质量m2=3kg,沙车的速度v1=2m/s,水平面光滑,不计小球与支架间的摩擦。
(i)若子弹打入小球A的过程用时△t=0.01s,求子弹与小球间的平均作用力;
(ii)求最终小车B的速度。
正确答案
F=784N,小车B速度为0.5m/s
解析
1、子弹打入小球的过程中,由动量守恒定律可得:
代入数据得:
以小球A为研究对象得:
代入数据得:
2、之后小球做平抛运动,以整个系统为研究对象,水平方向上动量守恒得:
代入数据得:
考查方向
动量守恒定律
解题思路
打击动量守恒,由动量守恒定律列方程求解
易错点
2问中小球做平抛运动,只有水平方向不受力,所以只有水平方向动量守恒
知识点
一昏迷病人由警察送来急诊,无发询问病史,但病人呼吸时有烂苹果味,可拟诊何病
A.酒醉
B.有机磷农药中毒
C.糖尿病酮症酸中毒
D.蛛网膜下腔出血
E.癔病
正确答案
C
解析
此题考查糖尿病酮症酸中毒的特征性表现,即呼气有烂苹果味(丙酮的气味)。酒精病人可闻到酒味。有机磷中毒病人呼气有大蒜味,瞳孔呈针尖样,癔病和蛛网膜下腔出血病人呼气没有特殊气味。
扫码查看完整答案与解析