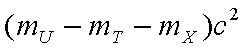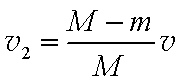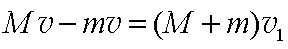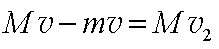- 动量守恒定律
- 共299题
(1)一群处于激发态n=4的氢原子,跃迁时可能发出_______种频率的光子;核反应方程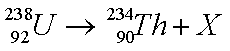
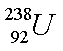
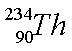
(2)如图所示,在光滑的水平面上,有一质量为M的长木板,长木板左端放一质量为m(M>m)的物块。现同时给长木板和物块相同大小的初速度v,分别向左、右运动。它们之间的动摩擦因数为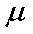
①物块和长木板相对静止时,物块的速度大小和方向;
②当物块的速度方向发生改变时,长木板的速度大小。
正确答案
(1)6;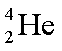
(2)①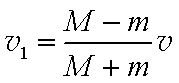
解析
(1)略。
(2)①设向左为正方向,对物块、长木板系统的运动,由动量守恒定律有:
解得:
由于M>m,因此,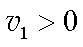
②设向左为正方向,物块的速度方向发生改变时也就是速度为0时,由动量守恒定律有:
解得:
知识点
(1)氦原子被电离出一个核外电子,形成类氢结构的氦离子.已知基态的氦离子能量为
A.54.4 eV(光子)
B.50.4 eV(光子)
C.48.4 eV(电子)
D.42.8 eV(光子)
E.41.8 eV(电子)
(2)如图所示,有n个相同的质点静止在光滑水平面上的同一直线上,相邻的两个质点间的距离都是1m,在某时刻给第一个质点一个初速度
正确答案
⑴ACE
⑵t=
解析
(1)由玻尔理论知,基态的氦离子要实现跃迁,入射光子的能量(光子能量不可分)应该等于氦离子在某激发态与基态的能量差,因此只有能量恰好等于两能级差的光子才能被氦离子吸收;而实物粒子(如电子)只要能量不小于两能级差,均可能被吸收.
氦离子在图示的各激发态与基态的能量差为:
Δ


Δ


Δ


Δ


可见,42.8eV和50.4eV的光子不能被基态氦离子吸收而发生跃迁.
(2)解:根据动量守恒可得:
得:
则相邻的两个质点间的运动时间表达式为:
∴经历的时间为:t=






知识点
下图为光电计时器的实验简易示意图。当有不透光物体从光电门间通过时,光电计时器就可以显示物体的挡光时间。光滑水平导轨MN上放置两个相同的物块A和B,左端挡板处有一弹射装置P,右端N处与水平传送带平滑连接,今将挡光效果好,宽度为d=3.6×10-3m的两块黑色磁带分别贴在物块A和B上,且高出物块,并使高出物块部分在通过光电门时挡光。传送带水平部分的长度L=8m,沿逆时针方向以恒定速度v=6m/s匀速转动。物块A、B与传送带间的动摩擦因数μ=0.2,质量mA=mB=1kg。开始时在A和B之间压缩一轻弹簧,锁定其处于静止状态,现解除锁定,弹开物块A和B,迅速移去轻弹簧,两物块第一次通过光电门,计时器显示读数均为t=9.0×10-4s,重力加速度g取10m/s2。试求:
(1)弹簧储存的弹性势能Ep;
(2)物块B在传送带上向右滑动的最远距离sm;
(3)若物块B返回水平面MN后与被弹射装置P弹回的物块A在水平面上相碰,且A和B碰后互换速度,则弹射装置P至少应以多大速度将A弹回,才能在AB碰后使B刚好能从Q端滑出?此过程中,滑块B与传送带之间因摩擦产生的内能△E为多大?
正确答案
(1)Ep=16J
(2)sm=4m
(3)△E=8(3
解析
(1)解除锁定,弹开物块A、B后,两物体的速度大小为:
vA=vB=
弹簧储存的弹性势能
(2)物块B滑上传送带做匀减速运动,当速度减为零时,滑动的距离最远。
由动能定理得:-μmBgsm=0-mBvB2/2
得 sm=4m
(3)B要刚好能滑出传送带的Q端,由能量关系有:

得: 
因为A和B碰撞过程交换速度,故弹射装置至少应以4
B在传送带上运动的时间
在B滑过传送带的过程中,传送带移动的距离:

△S=S带+L
因摩擦产生的内能为:△E=μmBg△S=8(3
知识点
(1)如图R为一含有




(2)如图所示,气球吊着A、B两个物体以速度v匀速上升,A物体与气球的总质量为m1,物体B的质量为m2,m1>m2。某时刻A、B间细线断裂,求当气球的速度为2v时物体B的速度大小并判断方向。(空气阻力不计)
正确答案
(1)β,4
(2)v2<0,物体的速度方向向下
解析
(1)略。
(2)根据动量守恒定律得:

解得:
∵m1>m2
∴v2<0,物体的速度方向向下
知识点
如图所示,光滑水平面上静止着一只木箱和一辆载人小车,已知木箱、小车、人的质量均相同。现人用力推动木箱,使木箱以速度v0水平向右运动,经过一段时间后,木箱与墙壁发生碰撞,碰撞之后木箱以原速率返回,人在车上抓住木箱之后,人、车、木箱不再分开,求木箱的最终速度大小。
正确答案
解析
取向左为正方向,由动量守恒定律有:
0=2mv1﹣mv0
得:
小明接木箱的过程中动量守恒,有:mv0+2mv1=(m+2m)v2
解得:
知识点
扫码查看完整答案与解析