椭圆的定义及标准方程
共448题

· 椭圆的定义及标准方程

椭圆的定义及标准方程
共448题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 13 分

20．已知椭圆：的左焦点，离心率为，函数，

（Ⅰ）求椭圆的标准方程；

（Ⅱ）设，，过的直线交椭圆于两点，求的最小值，并求此时的的值．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程

题型：简答题

简答题 · 13 分

20．已知椭圆C:的离心率为，以原点O为圆心，椭圆的短半轴长为半径的圆与直线相切

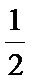
（Ⅰ）求椭圆C的标准方程

（Ⅱ）若直线L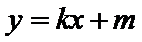：与椭圆C相交于A、B两点，且

求证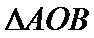：的面积为定值

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程直线与椭圆的位置关系直线与圆锥曲线的综合问题圆锥曲线的定点、定值问题

题型：简答题

简答题 · 12 分

21．已知圆:交轴于A,B两点,曲线是以AB为长轴,离心率为的椭圆,其左焦点为F,若P是圆上一点,连结PF,过原点作直线PF的垂线交直线x=-2于点Q.

（Ⅰ）求椭圆的标准方程；

（Ⅱ）当点P在圆上运动时（不与A、B重合）,求证:直线PQ与圆相切。

正确答案

解:（Ⅰ）因为,所以c=1,则b=1,

所以椭圆C的标准方程为

（Ⅱ）当点P在圆O上运动时,

设（）,则,

所以,,

所以直线OQ的方程为所以点Q（-2,）

所以,又

所以,即OP⊥PQ,

当，，故直线PQ始终与圆O相切

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程直线与圆锥曲线的综合问题直线、圆及圆锥曲线的交汇问题

题型：简答题

简答题 · 13 分

21．椭圆C：的离心率为，且过点（2,0）

（1）求椭圆C的方程；

（2）设直线：与椭圆C交于A．B两点，O为坐标原点，若OAB为直角三角形，求的值。

正确答案

解（1）依题意，可知，又，所以可知

∴

故所求的椭圆方程为

（2）联立方程消去得

则

解得

设

则，

① 若，则可知，即

∴

可解得

经检验满足条件

所以直线满足题意

② 若，则（或）

联立方程

解得或

Ⅰ．若A（，－），则可知－

Ⅱ．若B（－，），则可知

所以也满足题意

综上可知，及为所求的直线

另解:② 若，则（或）

联立方程解得

则点（在上,代入解得,所以也满足题意

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程

题型：单选题

单选题 · 5 分

8.椭圆的一个焦点是，那么实数的值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程

题型：单选题

单选题 · 5 分

9.已知，点P在A.B所在的平面内运动且保持，则的最大值和最小值分别是（）

A.3

B10.2

C5.1

D6.4

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程定义法求轨迹方程

题型：简答题

简答题 · 12 分

17.已知椭圆的对称轴为坐标轴，离心率，短轴长为，求椭圆的方程。

正确答案

或

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程

题型：简答题

简答题 · 12 分

21．已知椭圆的中心在原点，焦点在y轴上，离心率为，且椭圆经过圆的圆心C。

（1）求椭圆的标准方程；

（2）设直线与椭圆交于A，B两点，点且|PA|=|PB|，求直线的方程。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线的一般式方程椭圆的定义及标准方程直线与圆锥曲线的综合问题

题型：单选题

单选题 · 5 分

5．若椭圆的离心率为，则双曲线的离心率为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程

题型：简答题

简答题 · 13 分

20．设椭圆C：的左焦点为，上顶点为，过点作垂直于直线交椭圆于另外一点,交轴正半轴于点，且

（1）求椭圆的离心率；

（2）若过三点的圆恰好与直线l：相切，求椭圆C的方程。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程

继续学习学习下一知识点

下一知识点 : 椭圆的几何性质

百度题库 > 高考 > 文科数学 > 椭圆的定义及标准方程

扫码查看完整答案与解析