- 椭圆的定义及标准方程
- 共448题
已知椭圆C:
24.求椭圆C的方程及离心率;
25.设P为第三象限内一点且在椭圆C上,直线PA与y轴交于点M,直线PB与x轴交于点N,求证:四边形ABNM的面积为定值.
正确答案
由题意得,

所以椭圆

又
所以离心率
考查方向
解题思路
(1)由椭圆的几何性质公式进行计算
(2)将点设为
易错点
四边形的面积的计算,注意式子的正负
正确答案
设



又

直线

令


直线

令


所以四边形

从而四边形
考查方向
解题思路
(1)由椭圆的几何性质公式进行计算
(2)将点设为
易错点
四边形的面积的计算,注意式子的正负
5.已知点








正确答案
解析
设|F1F2|=2c,则可知|MF1|=2c,|MF2|=2


考查方向
本题考查椭圆的标准方程和简单几何性质。
解题思路
根据椭圆的焦点三角形是等腰直角三角形,结合椭圆的定义列方程可得。
易错点
无法根据图形确定方程。
教师点评
本题考查了椭圆知识,在近几年的各省高考题出现的频率较高,常与解三角形等知识点交汇命题。
知识点
12.一个圆经过椭圆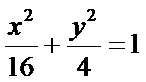
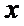
正确答案
解析
设圆心为(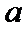

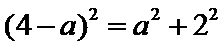
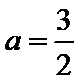
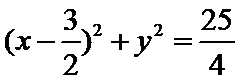
考查方向
圆和椭圆的基本知识.
解题思路
根据椭圆的标准方程,利用椭圆的性质,求出三个顶点的坐标,在直角坐标系中运用勾股定理求出圆心坐标、半径,代入圆的标准方程。
易错点
因为圆心在x轴的正半轴上,所以解方程时,注意舍去不合题意的根。
教师点评
本题属于简单题,意在考查学生对椭圆的标准方程和圆的标准方程知识掌握程度。
知识点
13. 过椭圆

正确答案
24
解析
由椭圆定义可得,
考查方向
解题思路
利用椭圆定义可得所求三角形的周长为4a。
易错点
记错椭圆定义出错。
知识点
已知椭圆


27.求椭圆方程;
28.若直线





正确答案
解析
由题意椭圆的离心率


∴椭圆方程为
又点

∴椭圆的方程为
考查方向
解题思路
由离心率求出,a,b,c的关系,用c表示出a,b来,再利用过点
易错点
熟悉a,b,c之间的关系。
正确答案
解析
设
消去

∵直线


又



设





将上式代入得
即



考查方向
解题思路
由直线与椭圆联立方程组,消去y,得到关于x的一元二次方程,有两不等实根,判别式大于零的不等式,又利用韦达定理可得,MN中点的坐标可以用,k,m表示。MN的垂直平分线过定点可得MN的中点在线段MN的垂直平分线上,这样可以得到k,m的等式,用等式与不等式联立,消去m的k的不等式,解不等式可得解。
易错点
利用韦达定理出错,以及垂直平分线过定点的利用。
扫码查看完整答案与解析

















