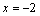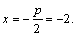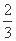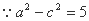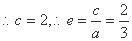椭圆的几何性质
共137题

· 椭圆的几何性质

椭圆的几何性质
共137题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 4 分

若抛物线的焦点与椭圆的右焦点重合，则该抛物线的准线方程为.

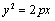
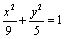
正确答案

解析

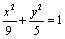
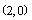
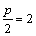
椭圆的右焦点右焦点为，故，故该抛物线的准线方程为

知识点

椭圆的几何性质

题型：简答题

简答题 · 12 分

已知抛物线C：与圆：有一个公共点，且在处两曲线的切线为同一直线上。

（1）求；

（2）设是异于且与及都切的两条直线，的交点为，求到的距离。

正确答案

见解析。

解析

（1）设，对求导得，故直线的斜率，当时，不合题意，所心

圆心为，的斜率

由知，即，解得，故

所以

（2）设为上一点，则在该点处的切线方程为即

若该直线与圆相切，则圆心到该切线的距离为，即，化简可得

求解可得

抛物线在点处的切线分别为，其方程分别为

① ② ③

②－③得，将代入②得，故

所以到直线的距离为。

知识点

椭圆的几何性质

题型：填空题

填空题 · 4 分

椭圆为定值，且的的左焦点为，直线与椭圆相交于点、，的周长的最大值是12，则该椭圆的离心率是______。

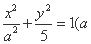
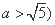
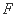
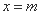
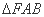
正确答案

解析

根据椭圆定义知：4a=12, 得a=3 , 又

知识点

椭圆的几何性质直线与椭圆的位置关系

题型：单选题

单选题 · 5 分

从椭圆(a＞b＞0)上一点P向x轴作垂线，垂足恰为左焦点F1，A是椭圆与x轴正半轴的交点，B是椭圆与y轴正半轴的交点，且AB∥OP(O是坐标原点)，则该椭圆的离心率是(　　)。

正确答案

解析

由题意知A(a,0)，B(0，b)，P，

∵AB∥OP，

∴.∴b＝c.

∵a2＝b2＋c2，∴.

∴.故选C。

知识点

椭圆的几何性质

题型：简答题

简答题 · 14 分

已知椭圆C：.

（1）求椭圆C的离心率；

（2）设O为原点，若点A在直线，点B在椭圆C上，且，求线段AB长度的最小值.

正确答案

（1）。

（2）长度的最小值为。

解析

（1）由题意，椭圆的标准方程为。

所以，，从而。

因此，，故椭圆的离心率。

（2）设点，的坐标分别为，，其中。

因为，

所以，

即，解得。

又，所以

。

因为，且当时等号成立，所以。

故线段长度的最小值为。

知识点

椭圆的几何性质直线与圆锥曲线的综合问题

继续学习学习下一知识点

下一知识点 : 椭圆的相关应用

百度题库 > 高考 > 文科数学 > 椭圆的几何性质

扫码查看完整答案与解析