- 抛物线焦点弦的性质
- 共82题
14.设抛物线


正确答案
知识点
20.已知抛物线





(1)若线段


(2) 若



正确答案
(1)
(2)
解析
本题属于圆锥曲线的基本问题,题目的难度是逐渐由易到难,
(1)由直线的参数表示出点
(2)根据弦长公式求出

(1)法一:
设



(1)当


(2)当

综上:
(1)法二:

设




(2)

考查方向
本题考查了求轨迹方程的方法、中点弦的处理方法、弦长公式及面积问题,常见求轨迹方程的方法有直译法、定义法、相关点法及参数法。圆锥曲线常见的问题有弦长、中点、面积、角度和“定”问题——定点、定线和定值。
易错点
1、求轨迹方程方法不熟练和点差法如何处理中点弦。
2、含参运算不正确导致出错。
知识点
13.抛物线








正确答案
解析
设抛物线方程



整理得
设直线与抛物线的两个交点的坐标分别为
由曲线与方程的定义,
由根与系数的关系得出两根之和
由抛物线的定义得出
解得
抛物线方程为
考查方向
解题思路
本题考查抛物线的定义,直线与圆锥曲线的位置关系,解题步骤如下:
(1)设抛物线方程
(2)写出直线的方程
(3)联立方程组由根与系数的关系得出两根之和;
(4)由抛物线的定义得出根与弦长的关系得解。
易错点
本题必须注意充分利用曲线的定义和设而不求,忽视而单纯运算则会出现错误。
知识点
13.抛物线








正确答案
解析
设抛物线

则
∵直线


∴可设直线

联立直线

消
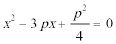
又∵
∴
∴抛物线方程为
考查方向
本题考查抛物线的简单性质,考查数形结合能力,注意解题方法的积累,属于中档题
解题思路
通过设抛物线

可得直线

联立直线方程和抛物线方程,
消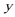
易错点
无
知识点
(4分)(2015•上海)抛物线y2=2px(p>0)上的动点Q到焦点的距离的最小值为1,则p= .
正确答案
2
知识点
扫码查看完整答案与解析






















