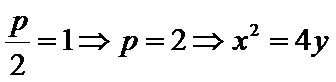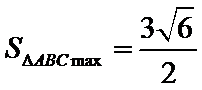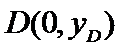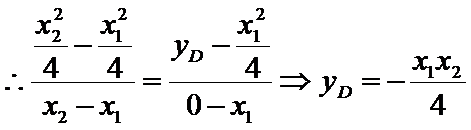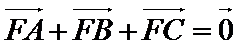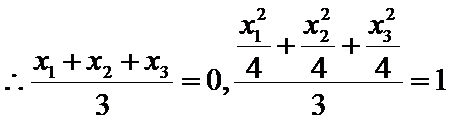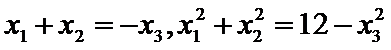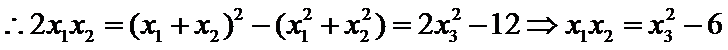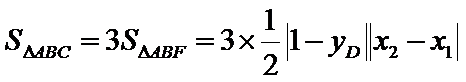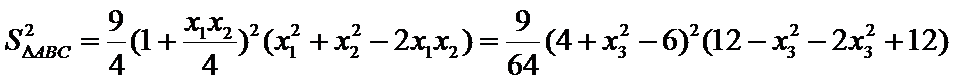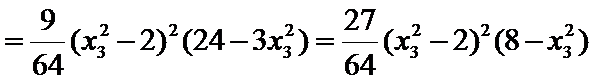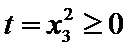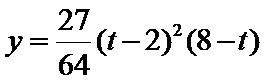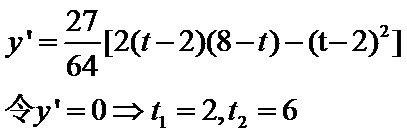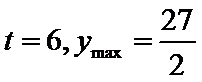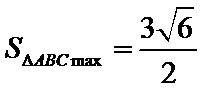- 抛物线焦点弦的性质
- 共82题
1
题型:简答题
|
已知点F(0,1)为抛物线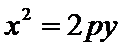
24.求抛物线C的方程;
25.点A、B、C是抛物线上三点且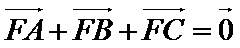
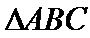
第(1)小题正确答案及相关解析
正确答案
(1)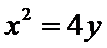
解析
(1)由题意知
考查方向
本题主要考查抛物线的标准准方程,直线与圆锥的关系。
解题思路
1)第一问利用抛物线的定义,可求出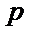
2)第二问首先设出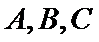
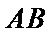
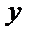
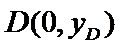
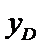
易错点
错位相减法求和计算容易错。
第(2)小题正确答案及相关解析
正确答案
(2)
解析
(2)令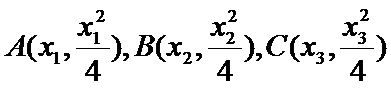
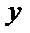
又因为
从而
令
当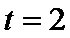
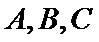
当
考查方向
本题主要考查抛物线的标准准方程,直线与圆锥的关系。
解题思路
1)第一问利用抛物线的定义,可求出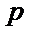
2)第二问首先设出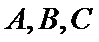
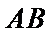
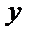
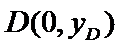
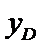
易错点
错位相减法求和计算容易错。
1
题型:简答题
|
20. 已知F(







(Ⅰ)求抛物线方程和N点坐标;
(Ⅱ)判断直线




正确答案
见解析
考查方向
抛物线的性质与特征,圆锥曲线中的最值问题
解题思路
建立适当的坐标系,利用直线斜率之间的关系建立方程,进而求解,与抛物线联立成方程组,整理可得。
易错点
计算能力弱,找不到面积最小时候的情况
知识点
抛物线焦点弦的性质
已完结
扫码查看完整答案与解析