- 进行简单的演绎推理
- 共9题
18.已知数列






















正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知集合M={



①M={
②M={
③M={
④M={
其中是“垂直对点集”的序号是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
设



(1)数表
(2) 数表

(3)对由



能否经过有限次“操作”以后,使得到的数表每行的各数之
和与每列的各数之和均为非负整数?请说明理由.
正确答案
见解析
解析
(1)解:法1:
法2:
法3:
…………………3分
(2)每一列所有数之和分别为2,0,

①如果首先操作第三列,则
则第一行之和为

这两个数中,必须有一个为负数,另外一个为非负数,
所以 
当
此时每列之和分别为
必有
当
此时第4列和为负,不符合题意. …………………6分
② 如果首先操作第一行
则每一列之和分别为


当
当


所以此时必须有


经检验,

综上:
(3)能经过有限次操作以后,使得得到的数表所有的行和与所有的列和均为非负实数。证明如下:
记数表中第











按要求操作一次时,使该行的行和(或该列的列和)由负变正,都会引起






知识点
设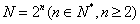
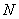
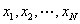

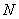
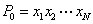

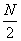
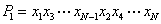
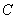
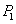
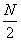
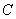
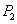
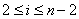
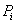
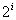
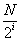
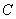
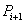
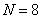
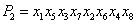
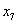
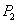
(1)当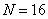
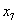
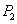
(2)当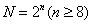
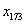
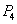
正确答案
(1)6
(2)
解析
(1)当N=16时,
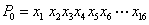
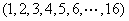
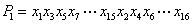
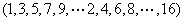
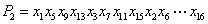
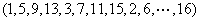
(2)方法同(1),归纳推理知x173位于P4中的第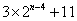
知识点
正偶数列有一个有趣的现象:
①2+4=6
②8+10 +12=14+16;
③18+20+22+24=26+28+30,…
按照这样的规律,则2016在第 个等式中。
正确答案
31
解析
略
知识点
扫码查看完整答案与解析